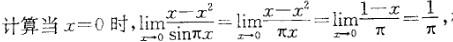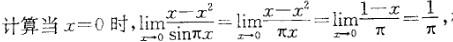x=2是函数y=x^2－1／x^2－3x＋2的()间断点。 A、可去B、跳跃C、无穷D、振荡
x=0是函数arctan1/x的( ).A.第二类间断点B.可去间断点C.跳跃间断点D.连续点
A.1个可去间断点，1个跳跃间断点B.1个可去间断点，1个无穷间断点C.2个跳跃间断点D.2个无穷间断点
设f(x)是不恒为零的奇函数,且f′(0)存在,则g(x)=().A.在x=0处无极限B.x=0为其可去间断点C.x=0为其跳跃间断点D.x=0为其第二类间断点
A.连续点B.无穷型间断点C.跳跃间断点D.可去间断点
A.连续点B.可去间断点C.跳跃间断点D.无穷间断点
函数的可去间断点个数为（ ）A.1B.2C.3D.无穷多个
函数 的可去间断点的个数为（ ）.A.1B.2C.3D.无穷多个
A.连续B.有可去间断点C.有跳跃间断点D.有无穷间断点
f(x)在［-1,1］上连续,则x=0是函数g(x)=的().A.可去间断点B.跳跃间断点C.连续点D.第二类间断点
设函数，则f(x)有A.1个可去间断点，1个跳跃间断点B.1个可去间断点，1个无穷间断点C.2个跳跃间断点D.2个无穷间断点
设则 x=1 是f(x)的：A.可去间断点 B.跳跃间断点 C.无穷间断点 D.振荡间断点
函数的无穷间断点的个数为（ ）A.0B.1C.2D.3
函数f(x)=(x-x2)/sinπx的可去间断点的个数为:A.1个B.2个C.3个D.无穷多个
A.可去间断点B.跳跃间断点C.无穷间断点D.振荡间断点
设f（x)为不恒等于零的奇函数，且厂(0)存在，则函数()。A、在x=0处左极限不存在B、有跳跃间断点x=0C、在x=0处右极限不存在D、有可去间断点x=0
函数可去间断点的个数为（ ）。A. 1 B. 2 C. 3 D.无穷多个
x=0点是函数y=lnx的（）。A、可去间断点B、连续点C、非可去第一类间断点D、第二类间断点
若x点是函数的可去间断点，则在x点处函数（）。A、左右极限都存在但不相等B、左极限不存在C、左右极限都存在且相等D、右极限不存在
x=0是函数的（）．A、第二类间断点B、可去间断点C、跳跃间断点D、连续点
x=1是函数arctan（1/1-x）的（）A、第二间断点B、可去间断点C、跳跃间断点D、连续点
单选题x=0点是函数y=lnx的（）。A可去间断点B连续点C非可去第一类间断点D第二类间断点
单选题x=1是函数arctan（1/1-x）的（）A第二间断点B可去间断点C跳跃间断点D连续点
单选题x=0是函数的（）．A第二类间断点B可去间断点C跳跃间断点D连续点
单选题点x＝0是函数y＝arctan（1/x）的（ ）。[2014年真题]A可去间断点B跳跃间断点C连续点D第二类间断点
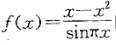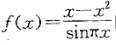的可去间断点的个数为：
