f(x)在[-1,1]上连续,则x=0是函数g(x)=的().A.可去间断点B.跳跃间断点C.连续点D.第二类间断点
f(x)在[-1,1]上连续,则x=0是函数g(x)=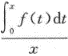 的().
的().
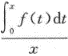 的().
的().
A.可去间断点
B.跳跃间断点
C.连续点
D.第二类间断点
B.跳跃间断点
C.连续点
D.第二类间断点
参考解析
解析:显然x=0为g(x)的间断点,因为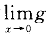 (x)=
(x)=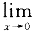
 =
=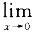 f(x)=f(0),所以x=0为g(x)的可去间断点,选(A)
f(x)=f(0),所以x=0为g(x)的可去间断点,选(A)
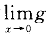 (x)=
(x)=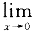
 =
=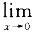 f(x)=f(0),所以x=0为g(x)的可去间断点,选(A)
f(x)=f(0),所以x=0为g(x)的可去间断点,选(A)
相关考题:
以下结论正确的是()。 A、若x0为函数y=f(x)的驻点,则x0必为函数y=f(x)的极值点.B、函数y=f(x)导数不存在的点,一定不是函数y=f(x)的极值点.C、若函数y=f(x)在x0处取得极值,且f′(x)存在,则必有f′(x)=0.D、若函数y=f(x)在x0处连续,则y=f′(x0)一定存在.
设函数f(x),g(x)在[a,b]上均可导(a<b),且恒正,若f′(x)g(x)+f(x)g′(x)>0,则当x∈(a,b)时,下列不等式中成立的是( )。 A. [f(x)/g(x)]>[f(a)/g(b)] B. [f(x)/g(x)]>[f(b)/g(b)] C. f(x)g(x)>f(a)g(a) D. f(x)g(x)>f(b)g(b)
下列命题正确的是()A.函数f(x)的导数不存在的点,一定不是f(x)的极值点B.若x0为函数f(x)的驻点,则x0必为f(x)的极值点C.若函数f(x)在点x0处有极值,且f'(x0)存在,则必有f'(x0)=0D.若函数f(x)在点x0处连续,则f'(x0)一定存在
(Ⅰ)证明拉格朗日中值定理:若函数f(x)在[a,b]上连续,在(a,b)内可导,则存在ξ∈(a,b),使得f(b)-f(a)=f'(ξ)(b-a);(Ⅱ)证明:若函数f(x)在x=0处连续,在(0,δ)(δ>0)内可导,且=A,则存在,且.
设函数f(x),g(x)是大于零的可导函数,且f′(x)g(x)-f(x)g′(x)<0,则当a<x<b时有( )《》( )A.f(x)g(b)>f(b)g(x)B.f(x)g(a)>f(a)g(x)C.f(x)g(x)>f(b)g(b)D.f(x)g(x)>f(a)g(a)
设f(x)在(-a,a)(a>0)上连续,F(x)是f(x)的一个原函数,则当f(x)是奇函数时,下面结论正确的是()。A、F(x)是偶函数B、F(x)是奇函数C、F(x)可能是奇函数,也可能是偶函数D、F(x)是否为奇函数不能确定
设f(x)在(-a,a)(a>0)上连续,F(x)是f(x)的一个原函数,则当f(x)是偶函数时,下面结论正确的是()。A、F(x)是偶函数B、F(x)是奇函数C、F(x)可能是奇函数,也可能是偶函数D、F(x)是否是偶函数不能确定
单选题(2008)设函数f(x)在(-∞,+∞)上是偶函数,且在(0,+∞)内有f′(x)0,f″(x)0则在(-∞,0)内必有:()Af′(x)0,f″(x)0Bf′(x)0,f″(x)0Cf′(x)0,f″(x)0Df′(x)0,f″(x)0
单选题设函数f(x),g(x)在[a,b]上均可导(a<b),且恒正,若f′(x)g(x)+f(x)g′(x)>0,则当x∈(a,b)时,下列不等式中成立的是( )。[2018年真题]Af(x)/g(x)>f(a)/g(b)Bf(x)/g(x)>f(b)/g(b)Cf(x)g(x)>f(a)g(a)Df(x)g(x)>f(b)g(b)
问答题设函数f(x),g(x)在[a,b]上连续,在(a,b)内可导,且对于(a,b)内一切x有f′(x)g(x)-f(x)g′(x)≠0。证明:如果f(x)在(a,b)内有两个零点,则介于两个零点之间,g(x)至少有一个零点。
问答题设函数f(x),g(x)二次可导,满足函数方程f(x)g(x)=1,又f′(x)≠0,g′(x)≠0,则f″(x)/f′(x)-f′(x)/f(x)=g″(x)/g′(x)-g′(x)/g(x)。