函数在x处的导数是
函数在x处的导数是
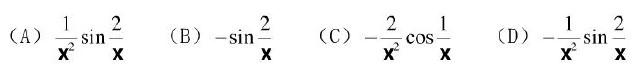
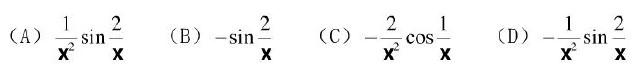
参考解析
解析:解:选A。
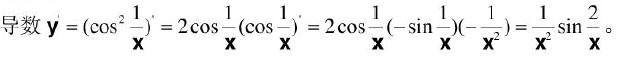
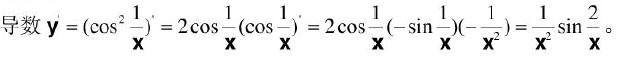
相关考题:
以下结论正确的是()。 A、若x0为函数y=f(x)的驻点,则x0必为函数y=f(x)的极值点.B、函数y=f(x)导数不存在的点,一定不是函数y=f(x)的极值点.C、若函数y=f(x)在x0处取得极值,且f′(x)存在,则必有f′(x)=0.D、若函数y=f(x)在x0处连续,则y=f′(x0)一定存在.
A.只能确定一个具有连续偏导数的隐函数z=z(x,y)B.可确定两个具有连续偏导数的隐函数y=y(x,y)和z=z(x,y)C.可确定两个具有连续偏导数的隐函数x=x(x,y)和z=z(x,y)D.可确定两个具有连续偏导数的隐函数x=x(y,z)和y=y(x,z)
函数y=(x)在点x=0处的二阶导数存在,且'(0)=0,"(0)>0,则下列结论正确的是().A.x=0不是函数(x)的驻点B.x=0不是函数(x)的极值点C.x=0是函数(x)的极小值点D.x=0是函数(x)的极大值点
下列命题正确的是()A.函数f(x)的导数不存在的点,一定不是f(x)的极值点B.若x0为函数f(x)的驻点,则x0必为f(x)的极值点C.若函数f(x)在点x0处有极值,且f'(x0)存在,则必有f'(x0)=0D.若函数f(x)在点x0处连续,则f'(x0)一定存在
单选题考虑二元函数f(x,y)的下面4条性质:①f(x,y)在点(x0,y0)处连续;②f(x,y)在点(x0,y0)处的两个偏导数连续;③f(x,y)在点(x0,y0)处可微;④f(x,y)在点(x0,y0)处的两个偏导数存在。若用“P⇒Q”表示可由性质P推出Q,则有( )。A②⇒③⇒①B③⇒②⇒①C③⇒④⇒①D③⇒①⇒④
单选题可微函数f(x,y)在点(x0,y0)取得极小值,下列结论正确的是( )。Af(x0,y)在y=y0处的导数等于零Bf(x0,y)在y=y0处的导数大于零Cf(x0,y)在y=y0处的导数小于零Df(x0,y)在y=y0处的导数不存在
判断题多元函数在某点处的偏导数刻划了函数在这点的变化率。A对B错