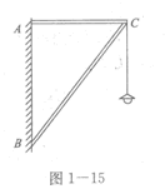
如图1—15所示，两根轻质细杆AC、BC用铰链固定在墙上构成一个直角三角形支架，在C处挂一盏吊灯。已知AC＝1．2 m，BC＝2 m，吊灯重200 N。求杆AC和BC所受力的大小和方向。

如图1—15所示，两根轻质细杆AC、BC用铰链固定在墙上构成一个直角三角形支架，在C处挂一盏吊灯。已知AC＝1．2 m，BC＝2 m，吊灯重200 N。求杆AC和BC所受力的大小和方向。

参考解析

解析：取C点为研究对象，分析其受力情况：绳子的拉力FT=G，AC杆的拉力FNl和BC杆的支持力

相关考题：

图示一起重机,A、B、C处均为光滑铰链,水平梁AB的重量P=4kN,荷载F=10kN,有关尺寸如图所示,BC杆自重不计。试求杆BC所受的拉力和铰链A给杆AB的约束力。
查看答案
图所示三角桁架由Q235钢制成，已知AB、AC、BC为1m，杆直径均为d=20mm，已知材料E=200GPa，σp=200MPa，σs=235MPa，a=304MPa，b=1.12MPa，稳定安全系数nst=3.0。试由BC杆的稳定性求这个三角架所能承受的外载F。
查看答案
在 △ABC中，∠C=90°，AB=10。（1）∠A=30°，求BC，AC（精确到0.01）；（2）∠A=45°，求BC，AC（精确到0.01）。
查看答案
试证明如下逻辑函数等式。(1) AB－＋AB－C=AB－;(2) AB(C＋C－)＋AC=AB＋AC;(3) A(BC＋BC)＋AC=A(BC)＋AC
查看答案
变截面杆AC受力如图。己知材料弹性模量为E，杆BC段的截面积为A，杆AB段的截面积为2A。杆C截面的轴向位移是（　　）。 A． FL/（2EA） B． FL/（EA） C． 2FL/（EA） D． 3FL/（EA）
查看答案
T形均质杆OABC以匀角速度ω绕O轴转动，如图所示。已知OA杆的质量为2m，长为2l，BC杆质量为m，长为l，则T形杆在该位置对O轴的动量矩为：
查看答案
如图所示，结构由AB、BC、CE三杆铰接而成，A处为固定端，杆重不计，铰C上作用一铅垂力P，则二力杆为（　　）。A．AB、BC、CEB．BC、CEC．ABD．均不是二力杆
查看答案
曲柄OA在如图30-9所示瞬时以ω的角速度绕轴O转动，并带动直角曲杆O1BC在如图所示平面内运动。若取套筒A为动点，杆O1BC为动系，则牵连速度大小为（　　）。
查看答案
T形均质杆OABC以匀角速度ω绕O轴转动，如图所示。已知OA杆的质量为2m，长为2l，BC杆质量为m，长为l，则T形杆在图示位置时动量的大小为：
查看答案
如图1—10所示，用绳子AC和BC吊起一重物处于静止状态。若AC能承受的最大拉力为150N，BC能承受的最大拉力为105N，OC绳能承受足够大的拉力，那么，下列说法正确的是（　　）A.当物重150N，AC、BC都不断，AC的张力比BC的张力大B.当物重150N，AC、BC都不断，AC的张力比BC的张力小C.当物重175N，AC不断，BC刚断后AC接着断D.当物重176N，BC断，AC不会断
查看答案
如图．已知圆⊙O是△ABC的外接圆，AD是圆⊙0的直径，且BD=BC，延长AD到E，且有∠EBD=∠CAB。 (1)求证：BE是⊙0的切线； (2)若BC=√3，AC=5，求圆的直径AD及切线BE的长。
查看答案
如图，在Rt△ACB中，∠ACB=90o,AC=15，BC=20，M是AB边上的动点(与A，B不重合)，N是BC上的动点(与B，C不重合)。 (1)当MN∥AC且BM=12．5时，求线段MN的长。 (2)当MN与AC不平行时，△CMN可能成为直角三角形吗?若可能，请写出线段CN长的取值范围；若不可能，请说明理由。
查看答案
在△ABC中，AB=2，BC=3，B=60°，BD为AC边上的高．求AC，BD．
查看答案
图示结构中AC杆的温度升高t℃，则杆AC与BC间的夹角变化是：A.增大B.减小C.不变D.不定
查看答案
在△ABC中，AB=2，BC=3，B=60°．求AC及△ABC的面积．
查看答案
如，在直角三角形ABC中，AC=4，BC=3，DE//BC，已知梯形BCDE的面积为3，则DE长为（ ）
查看答案
若将图4-15所示三铰刚架中AC杆上的力偶移至BC杆上，则A、B、C处的约束力（ ）。A.都改变 B.都不改变 C.仅C处改变 D.仅C处不变
查看答案
图示结构中BC和AC杆属于（ ）。A.压杆，拉杆B.压杆，压杆C.拉杆，拉杆D.拉杆，压杆
查看答案
所示桁架中AB和BC两杆的几何尺寸和受力如下，采用Q235。BC杆之间几何长度为4×1507mm，AB杆之间几何长度为2×2039mm。N2=-27.9kN（压力），N1=-24.9kN（压力），N3=-879.8kN（压力），N4=-859.3kN（压力），如图所示。若BC杆选用2180×110×12，短肢相并，间距12mm，iy=8.76cm，ix=5.78cm，A=67.4cm2，其稳定应力最接近（　　）N/mm2。A. 162.3 B. 168.4 C. 172.2 D. 195.6
查看答案
所示桁架中AB和BC两杆的几何尺寸和受力如下，采用Q235。BC杆之间几何长度为4×1507mm，AB杆之间几何长度为2×2039mm。N2=-27.9kN（压力），N1=-24.9kN（压力），N3=-879.8kN（压力），N4=-859.3kN（压力），如图所示。AB杆的平面外计算长度最接近（　　）m。A. 4.158 B. 3.968 C. 2.079 D. 1.984
查看答案
图3-31所示桁架中AB和BC两杆采用Q235钢，其几何尺寸和受力为：BC杆之间几何长度为4×1507mm，AB杆之间几何长度为2×2039mm；N2=－27.9kN（压力），N1=－24.9kN（压力），N3=－879.8kN（压力），N4=-859.3kN（压力）。AB杆的平面外计算长度接近（　　）m。A.1.984B.2.079C.3.968D.4.158
查看答案
图3-31所示桁架中AB和BC两杆采用Q235钢，其几何尺寸和受力为：BC杆之间几何长度为4×1507mm，AB杆之间几何长度为2×2039mm；N2=－27.9kN（压力），N1=－24.9kN（压力），N3=－879.8kN（压力），N4=-859.3kN（压力）。BC杆的平面外计算长度为（　　）m。A.2.996B.3.014C.5.994D.6.028
查看答案
所示桁架中AB和BC两杆的几何尺寸和受力如下，采用Q235。BC杆之间几何长度为4×1507mm，AB杆之间几何长度为2×2039mm。N2=-27.9kN（压力），N1=-24.9kN（压力），N3=-879.8kN（压力），N4=-859.3kN（压力），如图所示。BC杆的平面外计算长度最接近（　　）m。 A. 6.028 B. 5.994 C. 3.014 D. 2.996
查看答案
A.仅DE杆B.AC、BC、DE杆C.CD、CE、DE杆D.所有杆件
查看答案
有一镗削工件，三孔ABC的坐标尺寸如图，为检验上的需要，计算三孔ABC的中心距尺寸，正确的是（）。A、AB=26.93，BC=23.35，AC=27.2B、AB=26.93，BC=20.23，AC=26.5C、AB=25.03，BC=23.35，AC=27.2D、AB=25.03，BC=20.23，AC=27.2
查看答案
单选题社会总产值的价值构成可以用（　）表示。AC+VBC+MCV+MDC+V+M
查看答案
单选题如图所示，力P作用在BC杆的中点，且垂直于BC杆，若P=kN，杆重不计。则杆AB的内力大小S为（　）A 1kNB 0．5kNC 1．41kND 2kN
查看答案
热门标签