一正方形铁片面积为1平方米,用其剪出一个最大的圆,然后再圆中剪出一个最大的正方形,问新正方形的面积比原正方形的面积小多少?A.1/4平方米B.1/2平方米C.π/8平方米D.π/16平方米
一正方形铁片面积为1平方米,用其剪出一个最大的圆,然后再圆中剪出一个最大的正方形,问新正方形的面积比原正方形的面积小多少?
A.1/4平方米
B.1/2平方米
C.π/8平方米
D.π/16平方米
B.1/2平方米
C.π/8平方米
D.π/16平方米
参考解析
解析:第一步,本题考查几何问题,属于平面几何类。
第二步,由正方形铁片面积为1平方米,可知正方形的边长是1米,切割出的新正方形的对角线为最大圆的直径,即原正方形的边长。新正方形的边长为
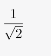
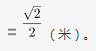
新正方形的面积为
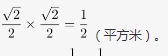
第三步,故新正方形的面积比原正方形小了

第二步,由正方形铁片面积为1平方米,可知正方形的边长是1米,切割出的新正方形的对角线为最大圆的直径,即原正方形的边长。新正方形的边长为
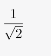
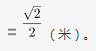
新正方形的面积为
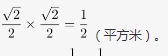
第三步,故新正方形的面积比原正方形小了

相关考题:
如图,一块边长为180厘米的正方形铁片,四角各被截去了 一个边长为40厘米的小正方形,现在要从剩下的铁片中剪 出一块完整的正方形铁片来,剪出的正方形面积最大为 ( )平方厘米。A. 16000 B. 16500C. 18000 D. 18600
如图,将正方形边长三等分后可得9个边长相等的小正方形,把中间的小正方形去掉,对剩下的8个小正方形,均按上面方法操作。问:对一个边长为2的正方形如此操作三次后所剩白色区域的面积是多少?A.B.C.D.
在一个正方形内画中、小两个正方形,使三个正方形具有公共顶点,这样大正方形被分割成了正方形区域甲,和L形区域乙、丙。已知三块区域甲、乙、丙的周长之比为4∶5∶7,并且区域丙的面积为48,求大正方形的面积:A 96B 98C 200D 102
单选题截面面积相等而其它条件相同的情况下,压杆的承载力最大的截面是()截面。A长方形B实心圆C正方形D空心圆