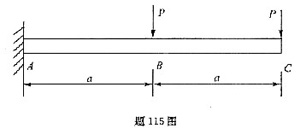
如图所示一悬臂梁，其抗弯刚度为FI，受两个力P的作用，则利用卡式定理求自由端C的挠度为( )。

如图所示一悬臂梁，其抗弯刚度为FI，受两个力P的作用，则利用卡式定理求自由端C的挠度为( )。



参考解析

解析：用卡式第二定理求，要将两个力加以区别

相关考题：

与加载初期比较,受弯构件在外荷载持续作用下,随着时间的延续() A、挠度增大B、挠度减小C、刚度B(也称为长期刚度)减小D、短期刚度减小
查看答案
两简支梁，一根为刚，一根为铜，已知它们的抗弯刚度相同。跨中作用有相同的力F，二者的()不同。A支反力B 最大正应力C 最大挠度D最大转角
查看答案
有如图所示简支梁，其抗弯刚度EI为常数。该梁的挠曲线方程为()。A.B.C.D.
查看答案
某悬臂梁其刚度为EI，跨度为l，自由端作用有力F。为减小最大挠度，则下列方案中最佳方案是()
查看答案
图示悬臂梁AD和BE的抗弯刚度同为EI=24×10^6N·m²，由杆CD相连接。CD杆的长度l=5m，截面积A=3×10^-4m²，E=200GPa。若FP=50kN，试求悬臂梁AD在D点的挠度。
查看答案
悬臂梁在自由端受集中力P作用，横截面形状和力P的作用线如图所示，其中产生斜弯曲与扭转组合变形的是哪种截面？A.矩形B.槽钢C.工字钢D.等边角钢
查看答案
两根矩形截面悬臂梁，弹性模量均为E，横截面尺寸如图，两梁的载荷均为作用在自由端的集中力偶。已知两梁的最大挠度相同，则集中力偶Me2是Me1的(悬臂梁受自由端集中力偶M作用，自由端挠度为ML2/2EI)A.8倍B.4倍C.2倍D.1倍
查看答案
已知图示两梁的抗弯截面刚度EI相同，若两者自由端的挠度相等，则P1/P2为:A.2B.4C.8D.16
查看答案
槽钢梁一端固定，一端自由，自由端受集中力P作用，梁的横截面和力P作用线如图所示(C点为横截面形心)，其变形状态为：A.平面弯曲B.斜弯曲C.平面弯曲加扭转D.斜弯曲加扭转
查看答案
已知图示梁抗弯刚度EI为常数，则用叠加法可得跨中点C的挠度为：
查看答案
用卡式定理计算如图所示梁C截面的挠度为( )。
查看答案
已知图示梁抗弯刚度EI为常数，则用叠加法可得自由端C点的挠度为：
查看答案
已知图示二梁的抗弯截面刚度EI相同，若二者自由端的挠度相等，则P1/P2为：A.2 B. 4 C. 8 D. 16
查看答案
已知图示二梁的抗弯截面刚度EI相同，若二者自由端的挠度相等，则P1/P2等于：（A）2(B)4(C)8(D)16
查看答案
悬臂梁受载如图所示，则其弯矩图为( )。
查看答案
已知刚架的弯矩图如图所示，杆的抗弯刚度为杆的为2EI，则结点B的角位移等于：
查看答案
图示组合结构，梁AB的抗弯刚度为EI，二力杆的抗拉刚度都为EA。DG杆的轴力为（　　）。 A、0 B、P，受拉 C、P，受压 D、2P，受拉
查看答案
如图所示的起重机平面简图，A端为止推轴承，B端为向心轴承，其自重为P1=40kN,起吊重物的重量为P2=100kN，试求A、B端的约束力。则：FNB=（ ）A.120kNB.一120kNC.60kND.—60kN
查看答案
已知图示二梁的抗弯截面刚度EI相同，若二者自由端的挠度相等，则P1/P2为：A.2B. 4C. 8D. 16
查看答案
用积分法求一悬臂梁受力后的变形时，边界条件为：在梁的固定端处（）。A、挠度为零，转角也为零B、挠度为零，转角不为零C、挠度不为零，转角为零D、挠度不为零，转角也不为零
查看答案
钢筋混凝土受弯构件挠度计算中采用的最小刚度原则是指在（）弯矩范围内，假定其刚度为常数，并按（）截面处的刚度进行计算。
查看答案
悬臂梁全梁受均布力的作用，其最大挠度中（）。A、自由端B、固定端C、中间D、1/3处
查看答案
作用均布荷载的悬臂梁，其（）挠度最大，（）转角最大。A、自由端处；固定端处B、自由端处；自由端处C、自由端处；跨中截面D、以上均不对
查看答案
两矩形截面悬臂梁，截面宽度相同，截面高度之比为2。若两梁材料相同，梁长之比为2，在自由端受相同集中力作用，则其最大挠度之比为1。
查看答案
两悬臂梁，其横截面和材料均相同，在梁的自由端作用有大小相等的集中力，但一梁的长度为另一梁的2倍，则长梁自由端的挠度是短梁的（）倍，转角又是短梁的（）倍。
查看答案
悬臂梁自由端受集中力F作用，其最大挠度在（）。A、固定端B、自由端C、中间D、1/3处
查看答案
单选题一长2000m的悬臂梁的自由端受集中力P=200kN作用，已知[σ]=150MPa，则此梁的危险截面的直径为（）mm。A290B280C310D300
查看答案
热门标签