若事件A1,A2,A3两两独立,则下列结论成立的是().
若事件A1,A2,A3两两独立,则下列结论成立的是().


参考解析
解析: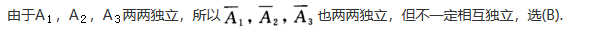
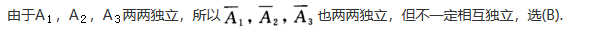
相关考题:
设a1,a2,a3,a4,a5是四维向量,则() A、a1,a2,a3,a4,a5一定线性无关B、a1,a2,a3,a4,a5一定线性相关C、a5一定可以由a1,a2,a3,a4线性表示D、a1一定可以由a2,a3,a4,a5线性表出
设向量组a1,a2,a3线性无关,则下列向量组中线性无关的是()。 A、a1-a2,a2-a3,a3-a1B、a1,a2,a3+a1C、a1,a2,2a1-3a2D、a2,a3,2a2+a3
设有栈S和队列Q,其初始状态为空,元素a1、a2、a3、a4、a5、a6依次入栈,出浅的元素则进入队列Q,若6个元素出列的顺序是a2、a4、a3、a6、a5、a1,则栈的容量至少是( )。A.6B.4C.3D.2
设A,B,C为三个事件,且A,B相互独立,则以下结论中不正确的是() A、若PC=1,则AC与BC也独立.B、若PC=1,则A并C与B也独立.C、若PC=0,则A并C与B也独立.D、若C属于B,则A与C也独立.
一个栈的入栈序列为a1,a2,a3,a4,a5,则此栈可能的输出序列是() A、a1,a2,a3,a4,a5B、a5,a4,a3,a2,a1C、a1,a5,a3,a4,a2D、a5,a1,a2,a3,a4
关系R(A1,A2,A3)上的函数依赖集F={A1A3→A2,A1A2→A3},若R上的一个分解为p={(A1,A2),(A1,A3)},则分解p()。A.是无损联接的B.是保持函数依赖的C.是有损联接的D.无法确定是否保持函数依赖
假设关系R(A1,A2,A3)上的函数依赖集F={A1→A2,A1→A3,A2→A3},则函数依赖()。A.A1→A2是冗余的B.A1→A3是冗余的C.A2→A3是冗余的D.A1→A2,A1→A3,A2→A3都不是冗余的
概率的基本性质有( )。A.概率是非负的,其数值介于0与1之间,即对任意事件A有0≤P(A)≤1B.C.P(A-B)=P(A)-P(B)D.P(A∪B)=P(A)+P(B)-P(AB)E.对于多个事件A1、A2、A3…有P(A1∪A2∪A3∪…)=P(A1)+P(A2)+P(A3)+…
设a1,a2,a3是3维列向量, A = a1,a2,a3 ,则与 A 相等的是:A. a1,a2,a3B. -a2,-a3,-a1C. a1+a2,a2+a3,a3+a1D. a1,a1+a2,a1+a2+a3
以下命题正确的是( ).A.若事件A,B,C两两独立,则三个事件一定相互独立B.设P(A)>0,P(B)>0,若A,B独立,则A,B一定互斥C.设P(A)>0,P(B)>0,若A,B互斥,则A,B一定独立D.A,B既互斥又相互独立,则P(A)=0或P(B)=0
若a1,a2,…,ar是向量组a1,a2,…,ar,…,an的最大无关组,则结论不正确的是:A. an可由a1,a2,…,ar线性表示B. a1可由 ar+1,ar+2,…,an线性表示C. a1可由a1,a2,…,ar线性表示D.an可由 ar+1 ,ar+2,,…,an线性表示
设a1,a2,a3是二维列向量, A = a1,a2,a3 ,则与 A 相等的是:A. a1,a2,a3 B. -a1,-a2,-a3 C. a1+a2,a2+a3,a3+a1 D. a1,a2,a1+a2+a3
设a1,a2,a3是三维列向量, A = a1,a2,a3 ,则与 A 相等的是:A. a1,a2,a3B. -a1,-a2,-a3C. a1+a2,a2+a3,a3+a1D. a1,a2,a1+a2+a3
已知al,a2,a3,a4是四维非零列向量,记A=(a1,a2,a3,a4),A+是A的伴随矩阵,若齐次方程组AX=0的基础解系为(1,0,-2,0)T,则AX=0的基础解系为( )。A、al a2B、a1 a3C、al a2 a3 D、a2 a3 a4
将一枚硬币独立地掷两次,引进事件:A1={掷第一次出现正面},A2={掷第二次出现正面},A3={正、反面各出现一次},A4={正面出现两次},则事件()A、A1,A2,A3相互独立B、A2,A3,A4相互独立C、A1,A2,A3两两独立D、A2,A3,A4两两独立
若R为关系模式名,A1、A2、A3、A4是其属性名,下列正确的关系模式表示形式是()A、R(A1×A2×A3×A4)B、R(A1,A2,(A3,A4))C、R(A1、A2、A3、A4)D、R(A1,A2,A3,A4)
问答题(1)已知A1,A2同时发生时A发生,证明:P(A)≥P(A1)+P(A2)-1。 (2)已知任意三个事件A1,A2,A3都满足Ai⊂A(i=1,2,3),证明:P(A)≥P(A1)+P(A2)+P(A3)-2。
单选题将一枚硬币独立地掷两次,以A1、A2、A3、A4依次表示事件“第一次出现正面”,“第二次出现正面”、“正、反面各出现一次”,“正面出现两次”,则事件( )。AA1,A2,A3相互独立BA2,A3,A4相互独立CA1,A2,A3两两独立DA2,A3,A4两两独立
问答题设试验E有4个基本事件,即s={w1,w2,w3,w4},并且它们发生是等可能的,又设A1={w1,w2},A2={w1,w3},A3={w1,w4},证明:A1,A2,A3两两独立,但不相互独立。