用消元法解方程组
用消元法解方程组

参考解析
解析: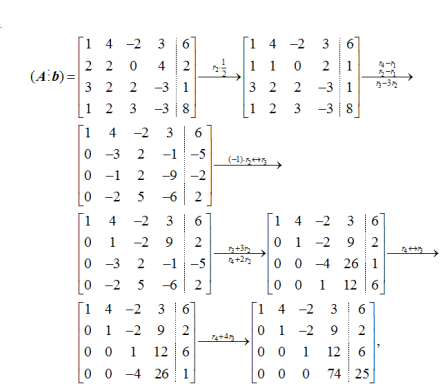
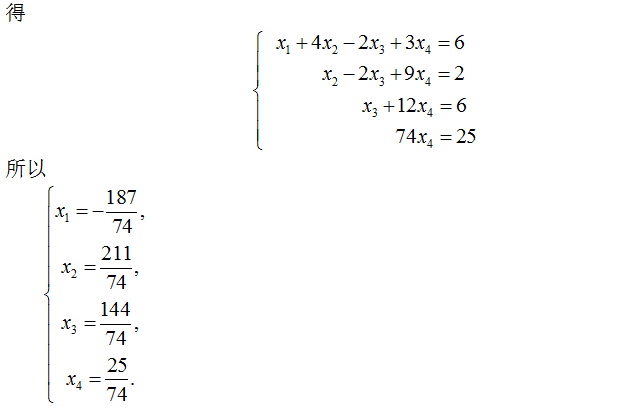

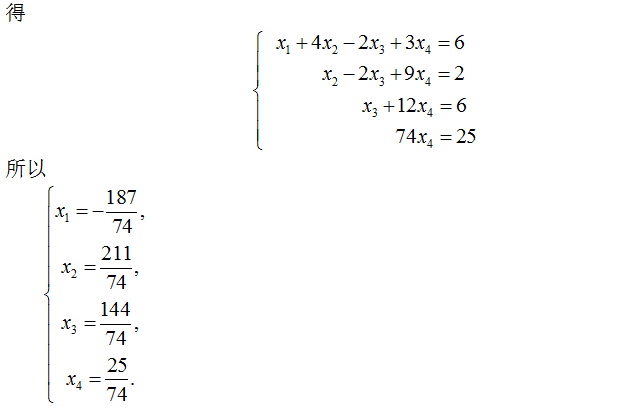
相关考题:
用列主元消元法解线性方程组x1+2x2+x3=02x1+2x2+3x+=3-x1-3x2=2作一次消元后得到的第三个方程为() A、-x2+x3=2B、-2x2+1.5x3=3.5C、-2x2+x3=3D、x2-0.5x3=-1.5
设A是m×n阶矩阵,下列命题正确的是().A.若方程组AX=0只有零解,则方程组AX=b有唯一解B.若方程组AX=0有非零解,则方程组AX=b有无穷多个解C.若方程组AX=b无解,则方程组AX=0一定有非零解D.若方程组AX=b有无穷多个解,则方程组AX=0一定有非零解
采用对流换热边界层微分方程组、积分方程组或雷诺类比法求解,对流换热过程中,正确的说法是( )。A. 微分方程组的解是精确解B. 积分方程组的解是精确解C. 雷诺类比的解是精确解D. 以上三种均为近似解
《代入法解二元一次方程组》一、面试考题试讲题目1.题目:代入法解二元一次方程组2.内容:3.基本要求:(1)试讲时间10分钟以内;(2)讲解要目的明确、条理清楚、重点突出;(3)根据讲解的需要适当板书;(4)结合例子归纳代入法解二元一次方程组的思路及步骤。答辩题目1.二元一次方程组有哪些解法?2.你是如何引导学生掌握二元一次方程组的解法的?注:图片节选自北京师范大学出版社初中数学八年级上册第109页
单选题采用对流换热边界层微分方程组,积分方程组或雷诺类比法求解对流换热过程中,正确的说法是( )。[2010年真题]A微分方程组的解是精确解B积分方程组的解是精确解C雷诺类比的解是精确解D以上三种均为近似值
填空题解线性方程组Ax=b的高斯顺序消元法满足的充要条件为()。