设袋中有5个球,其中3个新球,2个旧球,从中任取3个球,用X表示3个球中的新球个数,求X的分布律与分布函数.
设袋中有5个球,其中3个新球,2个旧球,从中任取3个球,用X表示3个球中的新球个数,求X的分布律与分布函数.
参考解析
解析: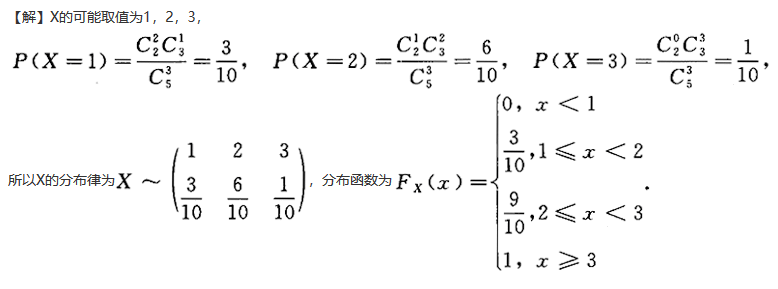
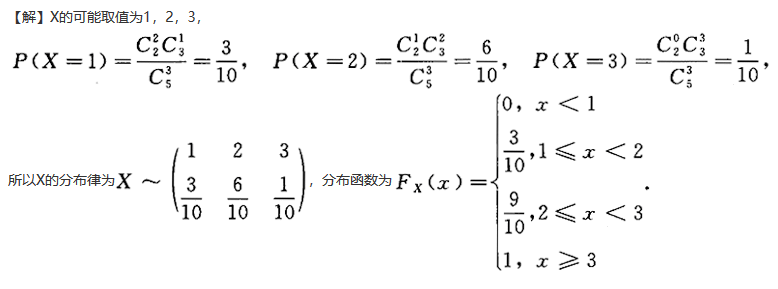
相关考题:
一个口袋内有4个不同的红球,6个不同的白球.(1)从中任取4个球,红球的个数不比白球少的取法有多少种?(2)若取一个红球记2分,取一个白球记1分,从中任取5个球,使总分不少于7分的取法有多少种?
有三个盒子,第一个盒子有4个红球1个黑球,第二个盒子有3个红球2个黑球,第三个盒子有2个红球3个黑球,如果任取一个盒子,从中任取3个球,以X表示红球个数. (1)写出X的分布律;(2)求所取到的红球数不少于2个的概率.
袋中有10个大小相等的球,其中6个红球4个白球,随机抽取2次,每次取1个,定义两个随机变量如下: 就下列两种情况,求(X,Y)的联合分布律: (1)第一次抽取后放回;(2)第一次抽取后不放回.
袋中有1个红球、2个黑球与3个白球,现有放回地从袋中取两次,每次取一个球.以X,Y,Z分别表示两次取球所取得的红球、黑球与白球的个数.(Ⅰ)求P{X=1|Z=0};(Ⅱ)求二维随机变量(X,Y)的概率分布.
袋中有l个红色球,2个黑色球与三个白球,现有放回地从袋中取两次,每次取一球,以 X,Y,Z分别表示丽次取球所取得的红球、黑球与白球的个数。 (1)求P{X=1|Z=0}; (2)求二维随机变量(X,Y)的概率分布。
一个口袋中有7个红球3个白球,从袋中任取一任球,看过颜色后是白球则放回袋中,直至取到红球,然后再取一球,假设每次取球时各个球被取到的可能性相同,求第一、第二次都取到红球的概率( )。A.7/10B.7/15C.7/20D.7/30
问答题袋中有四个球,分别标有数字1,2,2,3,从袋中任取一球后,不放回,再取第二次,分别以X、Y记为第一次、第二次取得球上标有的数字. 求:(1)(X,Y)的分布律. (2)(X,Y)的边缘分布律. (3)X与Y是否独立?
单选题袋中共有5个球,其中3个新球,2个旧球,每次取1个,无放回地取2次,则第二次取到新球的概率是().A3/5B3/4C1/2D3/10