利用施密特正交化方法把向量组a1=(0,1,1)′,a2=(1,1,0)′,a3=(1,0,1)′正交化
利用施密特正交化方法把向量组a1=(0,1,1)′,a2=(1,1,0)′,a3=(1,0,1)′正交化
参考解析
解析: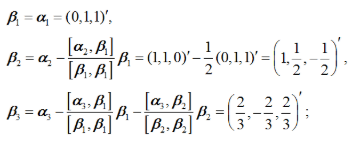
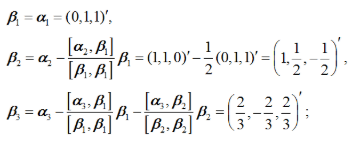
相关考题:
设向量组a1,a2,a3线性无关,则下列向量组中线性无关的是()。 A、a1-a2,a2-a3,a3-a1B、a1,a2,a3+a1C、a1,a2,2a1-3a2D、a2,a3,2a2+a3
设A为n阶实对称矩阵,则(). A.A的n个特征向量两两正交B.A的n个特征向量组成单位正交向量组C.A的k重特征值λ0,有r(λ0E-A)=n-kD.A的k重特征值λ。,有r(λ0E-A)=k
下述结论中,不正确的有() A.若向量a与β正交,则对任意实数a,b,aα与bβ也正交B.若向量β与向量a1,a2都正交,则β与a1,a2的任一线性组合也正交C.若向量a与正交,则a,β中至少有一个是零向量D.若向量a与任意同维向量正交,则a是零向量.
设a1,a2,a3是3维列向量, A = a1,a2,a3 ,则与 A 相等的是:A. a1,a2,a3B. -a2,-a3,-a1C. a1+a2,a2+a3,a3+a1D. a1,a1+a2,a1+a2+a3
3维向量组A:a1,a2,…,am线性无关的充分必要条件是( ).A.对任意一组不全为0的数k1,k2,…,km,都有k1a1+k2a2+…+kmam≠0B.向量组A中任意两个向量都线性无关C.向量组A是正交向量组D.
A. a1=(1,1,1,0)T,a2=(-1,-1,1,0)TB. a1=(2,1,0,1)T,a2=(-1,-1,1,0)TC. a1=(1,1,1,0)T,a2=(-1,0,0,0)TD.a1=(2,1,0,1)T,a2=(-2,-1,0,1)T
设A是三阶矩阵,a1(1,0,1)T,a2(1,1,0)T是A的属于特征值1的特征向量,a3(0,1,2)T是A的属于特征值-1的特征向量,则:A.a1-a2是A的属于特征值1的特征向量B.a1-a3是A的属于特征值1的特征向量C.a1-a3是A的属于特征值2的特征向量D. a1+a2+a3是A的属于特征值1的特征向量
设a1,a2,a3是二维列向量, A = a1,a2,a3 ,则与 A 相等的是:A. a1,a2,a3 B. -a1,-a2,-a3 C. a1+a2,a2+a3,a3+a1 D. a1,a2,a1+a2+a3
A. a1=(1,1,1,0)T,a2=(-1,-1,1,0)TB. a1=(2,1,0,1)T,a2=(-1,-1,1,0)TC. a1=(1,1,1,0)T,a2=(-1,0,0,0)TD. a1=(2,1,0,1)T,a2=(-2,-1,0,1)T
已知向量组a1==(3,2,-5)T,a2= (3,-1,3)T,a3 = (1,-1/3,1)T,a4 =(6,-2,6)T,则该向量组的一个极大线性无关组是:A.a2,a4B.a3,a4C.a1,a2D.a2,a3
设a1,a2,a3是三维列向量, A = a1,a2,a3 ,则与 A 相等的是:A. a1,a2,a3B. -a1,-a2,-a3C. a1+a2,a2+a3,a3+a1D. a1,a2,a1+a2+a3
在线性空间R3中,已知向量a1=(1,2,1),a2=(2,1,4),a3=(0,-3,2),记V1={λa1+μa2|λ,μ∈R},V2={ka3|k∈R}。令V3={t1η1+t2η2|t1,t2∈R,η1∈V1,η2∈V2}。(1)求子空间V3的维数;(2)求子空间V3的一组标准正交基。
已知al,a2,a3,a4是四维非零列向量,记A=(a1,a2,a3,a4),A+是A的伴随矩阵,若齐次方程组AX=0的基础解系为(1,0,-2,0)T,则AX=0的基础解系为( )。A、al a2B、a1 a3C、al a2 a3 D、a2 a3 a4
设向量组α1=(1,0,1)T,α2=(0,1,1)T,a3=(1,3,5)T,不能由向量组β1,=(1,1,1)T,f12=(1,2,3)T,3β=(3,4,α)T线性表示。(1)求a的值;(2)将β1β2β2由α1α2α3线性表示。
3维向量组A:α1,α2,…,αM线性无关的充分必要条件是().A、对任意一组不全为0的数k1,k2,…,kM,都有后B、向量组A中任意两个向量都线性无关C、向量组A是正交向量组D、αM不能由线性表示