某厂生产白水泥，对每一窑生产的水泥都需要测定其抗压强度，以确定水泥标号，一般是将水泥出窑后做成的试块养护28天所测得的数据为准。但是水泥不可能堆放28天后再出厂，所以考虑用7天的抗压强度x来预测28天的抗压强度y。现在统计了26窑的数据，求得的结果为：，假定在显著性水平a =0.05上查表得到相关系数的临界值为0.388，F分布的临界值为4. 26。对方程作显著性检验时，下列叙述正确的是（ ）。A.残差平方和的自由度为24 B.残差平方和的自由度为25C.检验统计量F的值为24. 986 D.检验统计量F的值为43. 074
某厂生产白水泥，对每一窑生产的水泥都需要测定其抗压强度，以确定水泥标号，一般是将水泥出窑后做成的试块养护28天所测得的数据为准。但是水泥不可能堆放28天后再出厂，所以考虑用7天的抗压强度x来预测28天的抗压强度y。现在统计了26窑的数据，求得的结果为：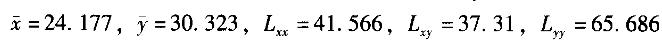
，假定在显著性水平a =0.05上查表得到相关系数的临界值为0.388，F分布的临界值为4. 26。
对方程作显著性检验时，下列叙述正确的是（ ）。
A.残差平方和的自由度为24 B.残差平方和的自由度为25
C.检验统计量F的值为24. 986 D.检验统计量F的值为43. 074
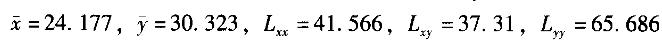，假定在显著性水平a =0.05上查表得到相关系数的临界值为0.388，F分布的临界值为4. 26。
对方程作显著性检验时，下列叙述正确的是（ ）。
A.残差平方和的自由度为24 B.残差平方和的自由度为25
C.检验统计量F的值为24. 986 D.检验统计量F的值为43. 074
参考解析
解析：根据题意得，n=26，所以总离差平方和的自由度为fT = n-1=25，回归平方和的自由度为fR =1，从而残差平方和的自由度为fE =fT-fR =24，检验统计量F的值为：
相关考题：
在研究某质量指标y对某物质的含量x的线性回归方程时，收集了10组数据，求得回归平方和为255.4，残差平方和为275，在α=0.05下，F分布的临界值为5.32，则有结论( )。A．F=4.32B．F=7.43C．回归方程不显著D．回归方程显著E．回归方程显著性无法判断
某厂生产白水泥，对每一窑生产的水泥都需要测定其抗压强度，以确定水泥标号，一般是将水泥做成的试块养护28天所测得的数据为准。但是水泥不可能堆放28天后再出厂，所以考虑用 7天的抗压强度x来预测28天的抗压强度y。现在统计了26窑的数据，求得如下结果：=24.177，=30.323，Lxx＝41.566，Lxy＝37.31，Lyy＝65.686又假定在显著性水平0.05查表得到相关系数的临界值为0.388，F分布的临界值为4.26。利用以上数据回答下列问题(1)～(6)：下列叙述正确的是( )。A．x与y的相关系数是0.014B．x与y的相关系数是0.714C．在0.05水平上y与x具有线性相关关系D．在0.05水平上y与x没有线性相关关系
在研究指标y与某物质的含量x的线性回归方程时，收集了10组数据，求得回归平方和为 255.4，残差平方和为27.5，在显著性水平0.05时F的临界值为5.32，则结论是( )。A．F＝9.287B．F＝74.30C．在0.05水平上方程不显著D．在0.05水平上方程显著E．F＝9.287
水泥标号是指标准水泥砂浆试体( )。A．在自然状态下，养护到测试时所达到的抗压强度B．在自然状态下，养护28天后达到的抗压强度C．在自然状态下，养护15天后达到的抗压强度D．在标准条件下，养护28天时达到的抗压强度
对某回归方程的某个回归系数进行显著性检验，经计算得到其t统计量值为5.8，如果相应的t分布的右侧临界值t0.025=2.447，则表明在0.05的显著性水平下，可以认为该变量对因变量有显著影响。A．正确B．错误
以0.05的显著性水平做总体均值的左侧检验,查t分布表得到的临界值为 1.74,则拒绝原假设的规则是()。 A.检验统计量大于1.74B.检验统计量小于于 1.74C.检验统计量大于- 1.74D.检验统计量小于- 1.74
某厂生产白水泥，对每一窑生产的水泥都需要测定其抗压强度，以确定水泥标号，一般是将水泥出窑后做成的试块养护28天所测得的数据为准。但是水泥不可能堆放28天后再出厂，所以考虑用7天的抗压强度x来预测28天的抗压强度y。现在统计了26窑的数据，求得的结果为：，假定在显著性水平α=0.05上查表得到相关系数的临界值为0.388，F分布的临界值为4.26。利用以上数据回答下列问题1～6：下列叙述正确的是( )。A．x与y的相关系数是0.014B．x与y的相关系数是0.714C．在0.05水平上y与x具有线性相关关系D．在0.05水平上y与x没有线性相关关系
根据下列材料，请回答下列各题 某厂生产白水泥，对每一窑生产的水泥都需要测定其抗压强度，以确定水泥标号，一般是将水泥做成的试块养护28天所测得的数据为准。但是水泥不可能堆放28天后再出厂，所以考虑用7天的抗Lxx=41.566，Lxy=37.31，Lyy=65.686 又假定在显著性水平0.05上查表得到相关系数的临界值为0.388，F分布的临界值为4.26。 利用以上数据回答下列问题(1)～(6)： 下面正确的叙述是（ ）。A.x与y的相关系数是0.014B.x与y的相关系数是0.714C.在0.05水平上y与x具有线性相关关系D.在0.05水平上y与x没有线性相关关系
对回归方程线性关系的显著性进行检验。其检验过程应包括( )。A．提出假设：原假设H0：β1=β2=…=βk=0；备择假设H1：β1，β2：，…，βk不全为零B．构造的统计量为：样本统计量服从自由度为(k，n-k-1)的F分布C．根据给定的显著性水平，确定临界值Fα(k，n-k-1)D．如果F＞Fα(k，n-k-1)，则拒绝原假设E．如果F＞Fα(k，n-k-1)，表明在(1-α)的置信概率下，模型的线性关系显著成立，模型通过方程显著性检验
某厂生产白水泥，对每一窑生产的水泥都需要测定其抗压强度，以确定水泥标号，一般是将水泥出窑后做成的试块养护28天所测得的数据为准。但是水泥不可能堆放28天后再出厂，所以考虑用7天的抗压强度x来预测28天的抗压强度y。现在统计了26窑的数据，求得的结果为：，假定在显著性水平a =0.05上查表得到相关系数的临界值为0.388，F分布的临界值为4. 26。下列叙述正确的是（ ）。A. x与y的相关系数是0.014B. x与y的相关系数是0.714C.在0. 05水平上y与x具有线性相关关系D.在0. 05水平上y与x没有线性相关关系
某厂生产白水泥，对每一窑生产的水泥都需要测定其抗压强度，以确定水泥标号，一般是将水泥出窑后做成的试块养护28天所测得的数据为准。但是水泥不可能堆放28天后再出厂，所以考虑用7天的抗压强度x来预测28天的抗压强度y。现在统计了26窑的数据，求得的结果为：，假定在显著性水平a =0.05上查表得到相关系数的临界值为0.388，F分布的临界值为4. 26。为求近似的预测区间需要得到a的估计，从上述数据得到此估计值为（ ）。 A. 0.982 B. 1.003 C. 1.134 D. 1.158
某厂生产白水泥，对每一窑生产的水泥都需要测定其抗压强度，以确定水泥标号，一般是将水泥出窑后做成的试块养护28天所测得的数据为准。但是水泥不可能堆放28天后再出厂，所以考虑用7天的抗压强度x来预测28天的抗压强度y。现在统计了26窑的数据，求得的结果为：，假定在显著性水平a =0.05上查表得到相关系数的临界值为0.388，F分布的临界值为4. 26。y关于x的一元线性回归方程= a+bx中，a与b分别为（ ）。A. a =3. 390； b= 1. 114 B. a =8. 612；b=0.898C. a =8. 612；b= 1. 114 D. a =8. 632；b=0.898
某厂生产白水泥，对每一窑生产的水泥都需要测定其抗压强度，以确定水泥标号，一般是将水泥出窑后做成的试块养护28天所测得的数据为准。但是水泥不可能堆放28天后再出厂，所以考虑用7天的抗压强度x来预测28天的抗压强度y。现在统计了26窑的数据，求得的结果为：，假定在显著性水平a =0.05上查表得到相关系数的临界值为0.388，F分布的临界值为4. 26。如果求得7天的抗压强度为26，那么可以预测28天的抗压强度为（）。A. 26.738 B. 31.96 C. 32.354 D. 35.576
在研究某质量指标y对某物质的含量x的线性回归方程时，收集了10组数据，求得回归平方和为255. 4，残差平方和为275，在α= 0. 05下，F分布的临界值为5.32，则有结论（ ）。A. F=4. 32 B. F=7. 43C.回归方程不显著 D.回归方程显著E.回归方程显著性无法判断
在研究某质量指标y对某物质的含量x的线性回归方程时，收集了10组数据，求得回归平方和为255. 4，残差平方和为275，在a=0.05下，F分布的临界值为5. 32，则有结论（ ）。A. F=4. 32 B. F = 7.43C.回归方程不显著 D.回归方程显著E.回归方程显著性无法判断
某厂生产白水泥，对每一窑生产的水泥都需要测定其抗压强度，以确定水泥标号，一般是将水泥出窑后做成的试块养护28天所测得的数据为准。但是水泥不可能堆放28天后再出厂，所以考虑用7天的抗压强度x来预测28天的抗压强度y。现在统计了26窑的数据，求得的结果为：，假定在显著性水平a =0.05上查表得到相关系数的临界值为0.388，F分布的临界值为4. 26。在对方程的总（离差）平方和作分解时，下列计算正确的是（ ）。A.回归平方和是33. 504 B.残差平方和为24. 123C.回归平方和是41. 563 D.残差平方和为32. 182
多选题在生产过程中，研究温度y与某物质的质量X的线性回归方程时，收集了l0组数据，求得回归平方和为255．4，残差平方和为27．5，在显著性水平0．05时，的临界值为5．32，则结论是( )。AF=9.287B在0.05水平上方程不显著CF=74.30D在0.05水平上方程显著E无法计算
多选题在研究某质量指标y对某物质的含量x的线性回归方程时，收集了10组数据，求得回归平方和为255.4，残差平方和为275，在α=0.05下，F分布的临界值为5.32，则有结论( )。AF=32BF=43C回归方程不显著D回归方程显著E回归方程显著性无法判断
单选题标号325号水泥指（）。A水泥7天抗压强度为325MpaB水泥7天抗压强度为32.5MpaC水泥28天抗压强度为32.5MpaD水泥28天抗压强度为325Mpa