某城市日用水量服从正态分布，现随机抽取5天的用水量作为样本，求得=169万吨；s=0. 50万吨，则总体标准差σ的95%的置信区间为（ ）。A. [0.2996，1.4374] B. [0.4607，1.3821]C. [0.5612，1.2219] D. [0.6025，1.2945]
某城市日用水量服从正态分布，现随机抽取5天的用水量作为样本，求得
=169万吨；s=0. 50万吨，则总体标准差σ的95%的置信区间为（ ）。
A. [0.2996，1.4374] B. [0.4607，1.3821]
C. [0.5612，1.2219] D. [0.6025，1.2945]
=169万吨；s=0. 50万吨，则总体标准差σ的95%的置信区间为（ ）。
A. [0.2996，1.4374] B. [0.4607，1.3821]
C. [0.5612，1.2219] D. [0.6025，1.2945]
参考解析
解析：正态总体标准差的1 - a置信区间为：
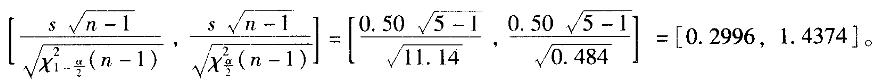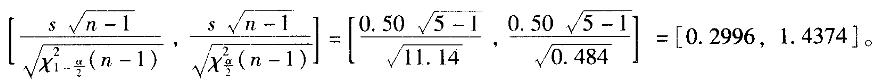17.
17.
相关考题：
某企业拟进行技术改造，减少老品种产量，生产新品种。现全厂年用水量为2万吨，如果不进行技术改造，全厂未来年用水量为2．5 万吨。如果进行技术改造，老品种年用水量为l万吨，新品种年用水量为2万吨。技术改造后公用设施等用水量增加，增加的比例为现全厂年用水量的10％，计算增量成本时应采用的年用“水量应为( )万吨。A．0．7B．1．0C．1．2D．1．5
从一个服从正态分布的总体中随机抽取样本容量为n的样本，在95%的置信度下对总体参数进行估计的结果为：20±0.08。如果其他条件不变，样本量扩大到原来的4倍，则总体参数的置信区间应该是（ ）。A.20±0.16B.20±0.04C.80±0.16D.80±0.04
从一个正态总体中随机抽取一个容量为n的样本,其均值和标准差分别为50和8。当n=25时,构造总体均值μ的95%置信区间为()。 A、50±3.16B、50±4.97C、50±1.65D、50±1.96
某溶液中的乙醇浓度服从正态分布，从中抽取一个样本量为4的样本，求得=8.5，样本标准差为s=0.04，则正态均值μ与σ的95%的置信区间分别为( )。A．[8.292，8.550]；[0.017，0.112]B．[8.430，8.550]；[0.023，0.112]C．[8.436，8.564]；[0.023，0.149]D．[8.449，8.564]；[0.017，0.149]
某城市日用水量服从正态分布，现随机抽取5天的用水量作为样本，求得=169万吨；s=0.50万吨，则总体标准差σ的95%的置信区间为( )。A．[0.2996，1.4374]B．[0.4607，1.3821]C．[0.5612，1.2219]D．[0.6025，1.2945]
假设某总体服从正态分布N(12, 4)，现从中随机抽取一容量为5的样本X1,X2, X3, X4, X5，则：样本均值与总体均值之差的绝对值大于1的概率是（）。A. 0.2628 B. 0. 98 C. 0.9877 D. 0.9977
某溶液中的乙醇浓度服从正态分布，从中抽取一个样本量为4的样本，求得=8.5， 样本标准差为s=0. 04，则正态均值μ与σ的95%的置信区间分别为（ ）。A. [8.292，8.550] ； [0.017，0.112] B. [8.430，8.550]；[0.023，0. 112]C. [8.436，8.564] ； [0.023，0. 149] D. [8.449，8.564]；[0.017，0. 149]
已知总体服从方差为25的正态分布，样本容量为100，样本均值为165，则总体均值95.45%（Z0.025=2）的置信区间是（）。A．164-166B．163-167C．162-168D．161-169
从一个服从正态分布的总体中随机抽取样本容量为n的样本，在95％的置信度下对总体均值进行估计的结果为20±0.08。如果其他条件不变，样本容量扩大到原来的4倍，则总体均值的置信区间应该是( )。A.20±0.16B.20±0.04C.80±0.16D.80±0.04
已知某测验结果服从正态分布，总体方差σ2＝16，从中随机抽取 100 名被试，其平均值则总体平均值μ的 95%的置信区间为（）A.76.97＜μ＜78.03B.77.51＜μ＜78.49C.77.2＜μ＜78.78D.76.36＜μ＜78.64
设某人群的身高X服从N（155.4，5.32）分布，现从该总体中随机抽出一个n=10的样本，得均值为X=158.36，S=3.83，求得μ的95%可信区间为（155.62，161.10），发现该区间竟然没有包括真正的总体均数155.4。若随机从该总体抽取含量n=10的样本200个，每次都求95%置信区间，那么类似上面的置信区间（即不包括155.4在内）大约有（）.A、5个B、20个C、10个D、1个E、190个
某企业拟进行技术改造，减少老品种产量，生产新品种。现全厂年用水量为2万吨，如果不进行技术改造，全厂未来年用水量为2.5万吨。如果进行技术改造，老品种年用水量为1万吨，新品种年用水量为2万吨。技术改造后公用设施等用水量增加，增加的比例为现全厂年用水量的10%，计算增量成本时应采用的年用水量为（）万吨。A、0.7B、1.0C、1.2D、1.5
单选题某企业拟进行技术改造，减少老品种产量，生产新品种。现全厂年用水量为2万吨，如果不进行技术改造，全厂未来年用水量为2.5万吨。如果进行技术改造，老品种年用水量为l万吨，新品种年用水量为2万吨。技术改造后公用设施等用水量增加，增加的比例为现全厂年用水量的10%，计算增量成本时应采用的年用水量应为（ ）万吨。A0.7B1.0C1.2D1.5