使用P控制图的样本量n = 100，其UCLp与CLp的间距设为1。当n改为400时，设不变，UCLp与CLp的间距调整为（ ）。A. 1/4 B. 4/1 C. 1/2 D. 2/1

使用P控制图的样本量n = 100，其UCLp与CLp的间距设为1。当n改为400时，设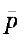不变，UCLp与CLp的间距调整为（ ）。A. 1/4 B. 4/1 C. 1/2 D. 2/1

参考解析

解析：

相关考题：

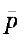使用p控制图的样本量n=100，其UCLp与CLp的间距设为1。当n改为400时，设p不变，UCLp与CLp的间距调整为( )。A．1/4B．4/1C．1/2D．2/1
查看答案
若i1=2i2，n1=n2/2，则当P相同时，（ ）。A．（F/P，i1，n1）（F/P，i2，n2）B．（F/P，i1，n1）=（F/P，i2，n2）C．（F/P，i1，n1）（F/P，i2，n2）D．不能确定（F/P，i1，n1）与（F/P，i2，n2）的大小
查看答案
设X～N(1，4)，为样本容量n＝16的样本均值，则P(0＜≤2)为( )。A．2Φ(0.5-1)B．2Φ(2)-1C．2u0.5-1D．1-2Φ(2)
查看答案
正态分布计算所依据的重要性质为( )。A．设X～N(μ,σ2)，则u=(X-μ)/σ～N(0，1)B．设X～N(μ，σ2)，则对任意实数a、b有P(X＜b)=Ф[(b-μ)/σ)C．设X～N(μ，σ2)，则对任意实数a、b有P(X＞a)=1-Ф[(a-μ)/σ]D．设X～N(μ，σ2)，则对任意实数a、b有P(a＜X＜b)=Ф[(b-μ)/σ)-Ф[(a-μ)/σ]E．设X～μ(μ1，，Y～N(μ2，，则X+Y～N(μ1+μ2，(σ1+σ2) 2)
查看答案
设X～N(80，202)，为样本容量n＝100的样本均值，则P(|-80|≥3)为( )。A．2Φ(1.5)-1B．1-2Φ(3)C．2-2Φ(1.5)D．2-2Φ(3)
查看答案
设Xi=(i=1，2，…，16)为正态总体N(0，4)的样本，为样本均值，则的分布可以表示为( )。A．N(0，1/2)B．N(0，4)C．N(0，1/4)D．概率密度为E．N(0，1/8)
查看答案
设X～N(1，4)，为样本容量n=16的样本均值，则P(0＜≤2)为( )。A．2Ф(0.5)-1B．2Ф(2)-1C．1-2Ф(0.5)D．1-2Ф(2)
查看答案
样本含量分别为n1和n2的两样本率分别为P1和P2，其合计率Pt的计算公式为A.Pl+P2B.(Pl+P2)／2C.(P1+P2)／ND.nlP1+n2P2/n1+n2E.P1+P2/n1n2
查看答案
设X-N(5,4)，则P(2A.φ(1.5)-φ(1)B.φ(1)-φ(1.5)C.φ(-1)-φ(-1.5)D.φ(-1.5)-φ(-1)
查看答案
关于排列n(n1)…2 1的奇偶性，以下结论正确的是（ ）.A.当n为偶数时是偶排列B.当n为奇数时是奇排列C.当n=4m或n=4m+2时是偶排列D.当n=4m或n=4m+1时是偶排列，当n=4m+2或n=4m+3时奇排列
查看答案
设X~N(1，4)，则P(0≤XA. 2Φ(0.5) -1 B. 1-2Φ(0.5) C. 2u0.5 -1 D. 1 -2u0.5
查看答案
设X~N(1，4), 为样本容量n = 16的样本均值，则P(0≤2)为（ ）。A. 2Φ(0.5)-1 B. 2Φ(2) -1 C. 1-2Φ(0.5) D. 1 -2Φ(2)
查看答案
设Xi=(i= 1, 2, …,16)为正态总体N(0，4)的样本，为样本均值，则的分布可以表示为（）。A. N(0, 1/2) B. N(0, 4)C. N(0, 1/4)E. N(0, 1/8)
查看答案
从正态总体N(10，22)中随机抽出样本量为4的样本，则样本均值的标准差为（）。A. 0.5 B. 1 C. 2 D. 4
查看答案
已知X~N(1, 22)，Y~N(3, 42)，则P1=P1(02 =P(3 A. P12 B. P1>P2 C. P1=4P2 D. P1=P2
查看答案
设随机变量X～N(0,σ^2),Y～N(0,4σ^2),且P(X≤1,y≤-2)=,则P（X>1,Y>-2）=_______.
查看答案
设集合M＝{0，1，2，3，4)，N＝{1，2，3)，T＝{2，4，6)，则集合(M∩T)∪N＝（　　）A.{0，1，2，3，4，6}B.{1，2，3，4}C.{2，4}D.{2，4，6}
查看答案
设集合M＝{1，2，4)，N＝{2，3，5)，则集合M∪N＝（　　）A.{2}B.{1，2，3，4，5}C.{3，5}D.{1，4}
查看答案
设集合P={x｜-1≤x≤3｝，N={x｜2≤x≤4)，则P∪N是( )A.{x｜2≤x≤3}B.{x｜2C.{x｜-1D.{x｜-1≤x≤4｝
查看答案
X－R控制图适用于样本量（ ）的情况。A. n = 1 B. 1C. n>10 D. n>20
查看答案
样本含量分别为n1和n2的两样本率分别为p1和p2，则其合并平均率pc为（）A、P1+P2B、（P1+P2）/2C、P1×P2D、（n1P1+n2P2）/（n1+n1）E、（n1-1）p1+（n2-1）P2/（n1+n2-2）
查看答案
免疫球蛋白（IgG）多肽的可变区为（）A、N端轻链的1/4与重链的1/2B、N端轻链的1/3与重链的1/4C、N端轻链的1/2与重链的1/4D、N端轻链的1/2与重链的1/2E、N端轻链的1/2与重链的1/3
查看答案
设p是一个素数，且p≡-1（mod4）则Zp的所有非零平方元的集合D是Zp的加法群的什么差集？（）A、（4n-1，2n，n）B、（4n-1，2n-1，n-1）C、（4n+1，2n-1，n-2）D、（4n-1，2n+1，n-3）
查看答案
样本含量分别为n1和n2的两样本率分别为P1和P2，则其合并平均率PC为（）A、P1+P2B、（P1+P2）／2C、p1xP2D、（n1P1+n2P2）／（n1+n1）E、（n1-1）P1+（n2-1）P2／（n1+n2-2）
查看答案
单选题样本含量分别为n1和n2的两样本率分别为p1和p2，则其合并平均率pc为（）AP1+P2B（P1+P2）/2CP1×P2D（n1P1+n2P2）/（n1+n1）E（n1-1）p1+（n2-1）P2/（n1+n2-2）
查看答案
单选题样本含量分别为n1和n2的两样本率分别为p1和p2，则其合并平均率PC为（　　）。APl+P2B(Pl+P2)/2CPl×P2D(n1 P1+n2P2)/(nl+n2)E(nl－1)Pl+(n2－1)P2/(nl+n2－2)
查看答案
单选题样本含量分别为n1和n2的两样本率分别为P1和P2，则其合并平均率PC为（）AP1+P2B（P1+P2）／2Cp1xP2D（n1P1+n2P2）／（n1+n1）E（n1-1）P1+（n2-1）P2／（n1+n2-2）
查看答案
热门标签