已知函数y=f(x)在x1和x2处的值分别为y1和y2,其中,x2>x1且x2-x1比较小(例如0.01),则对于(x1,x2)区间内的任意x值,可用线性插值公式()近似地计算出f(x)的值A.y1+(y2-y1)(x-x1)/(x2-x1)B.x1+(y2-y1)(x-x1)/(x2-x1)C.y2+(y2-y1)(x2-x1)/(x-x1)D.x2+(x2-x1)(x-x1)/(y2-y1)
已知函数y=f(x)在x1和x2处的值分别为y1和y2,其中,x2>x1且x2-x1比较小(例如0.01),则对于(x1,x2)区间内的任意x值,可用线性插值公式()近似地计算出f(x)的值
A.y1+(y2-y1)(x-x1)/(x2-x1)
B.x1+(y2-y1)(x-x1)/(x2-x1)
C.y2+(y2-y1)(x2-x1)/(x-x1)
D.x2+(x2-x1)(x-x1)/(y2-y1)
B.x1+(y2-y1)(x-x1)/(x2-x1)
C.y2+(y2-y1)(x2-x1)/(x-x1)
D.x2+(x2-x1)(x-x1)/(y2-y1)
参考解析
解析:线性插值是数学、计算机图形学等领域广泛使用的一种简单插值方法假设我们已知坐标(x0,y0)与(x1,y1),要得到[x0,x1]区间内某一位置x在直线上的y值。
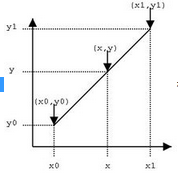
根据图中所示,假设AB上有一点(x,y),可作出两个相似三角形,我们得到(y-y0)/(y1-y0)=(x-x0)/(x1-x0)。因此结合本题结果为y=y1 +(y2-y1 )(x-x1 )/(x2-x1 )。

根据图中所示,假设AB上有一点(x,y),可作出两个相似三角形,我们得到(y-y0)/(y1-y0)=(x-x0)/(x1-x0)。因此结合本题结果为y=y1 +(y2-y1 )(x-x1 )/(x2-x1 )。
相关考题:
已知x1(t)和x2(t)的傅里叶变换分别为X1(f)和X2(f),则卷积x1(t)*x2(t)的傅里叶变换为()。 A、X1(f)X2(f)B、X1(f)*X2(f)C、X1(-f)X2(-f)D、X1(-f)*X2(-f)
阅读以下说明和C++代码,[说明]现要编写一个画矩形的程序,目前有两个画图程序:DP1和DP2,DP1用函数draw_a_line(x1,y1,x2,y2)画一条直线,DP2则用drawline(x1,x2,y1,y2)画一条直线。当实例化矩形时,确定使用DP1还是DP2。为了适应变化,包括“不同类型的形状”和“不同类型的画图程序”,将抽象部分与实现部分分离,使它们可以独立地变化。这里,“抽象部分”对应“形状”,“实现部分”对应“画图”,与一般的接口(抽象方法)与具体实现不同。这种应用称为Bridge(桥接)模式。图6-1显示了各个类间的关系。[图6-1]这样,系统始终只处理3个对象:Shape对象、Drawingg对象、DP1或DP2对象。以下是C++语言实现,能够正确编译通过。[C++代码]class DP1{public:static void draw_a_line(double x1,double y1,double x2,double y2){//省略具体实现}};class DP2{public:static void drawline(double x1,double x2,double y1,double y2){//省略具体实现}};class Drawing{public:(1) void drawLine(double x1,double y1,double x2,double y2)=0;};class V1Drawing:public Drawing{public:void drawLine(double x1,double y1,double x2,double y2){DP1::draw_a_line(x1,y1,x2,y2);}};class V2Drawing:public Drawing{public:void drawLine(double x1,double y1,double x2,double y2){(2)}};class Shape{privatc:(3) dp;public:Shape(Drawing*dp);virtual void draw()=0;void drawLine(double x1,double y1,double x2,double y2);};Shape::Shape(Drawing*dp){_dp=dp;}void Shape::drawLine(double x1,double y1,double x2,double y2){ //画一条直线(4);}class Rectangle:public Shape{privatc:double_x1,_y1,_x2,_y2;public:Rectangle(Drawing *dp,double x1,double y1,double x2,double y2);void draw();};Rectangle::Rectangle(Drawing*dp,double x1,double y1,double x2,double y2): (5){_x1=x1;_y1=yl;_x2=x2;_y2=y2;}void Rectangle::draw(){//省略具体实现}(1)
如果一个直线控件在窗体上呈现为一条垂直线,则可以确定的是( )。A.它的Y1、Y2属性的值相等SXB 如果一个直线控件在窗体上呈现为一条垂直线,则可以确定的是( )。A.它的Y1、Y2属性的值相等B.它的 X1、X2属性的值相等C.它的X1、Y1属性的值分别与X2、Y2属性的值相等D.它的 X1、X2属性的值分别与Y1、Y2属性的值相等
阅读以下说明和c++代码,将应填入(n)处的字句写在对应栏内。【说明】现要编写一个画矩形的程序,目前有两个画图程序:DP1和DP2,DP1用函数draw_a_line(x1, y1,x2,y2)画一条直线,DF2则用drawline(x1,x2,y1,y2)画一条直线。当实例画矩形时,确定使用DP1还是DP2。为了适应变化,包括“不同类型的形状”和“不同类型的画图程序”,将抽象部分与实现部分分离,使它们可以独立地变化。这里,“抽象部分”对应“形状”,“实现 部分”对应“画图”,与一般的接口(抽象方法)与具体实现不同。这种应用称为Bridge(桥接)模式。图9-7显示了各个类间的关系。这样,系统始终只处理3个对象:Shape对象、Drawing对象、DP1或DP2对象。以下是 C++语言实现,能够正确编译通过。【C++代码】class DP1{public:static void draw_a_line(double x1, double y1,double x2, double y2){//省略具体实现});class DP2{public:static void drawline(double x1, double x2,double y1, double y2){//省略具体实现}};class Drawing{public:(1) void drawLine(double x1,double y1,double x2,double y2)=0;};class V1Drawing:public Drawing{public:void drawLine(double x1, double y1,double x2, double y2){DP1::draw_a_line(x1,y1,x2,y2);}};class V2Drawing:public Drawing{public:void drawLine(double x1, double y1, double x2, double y2){(2);}};class Shape{private:(3) _dp;public:Shape(Drawing *dp);virtual void draw()=0;void drawLine(double x1, double y1, double x2, double y2);};Shape::Shape(Drawing *dp){_dp = dp;}void Shape::drawLine(double x1, double y1, double x2, double y2){ //画一条直线(4);}class Rectangle: public Shape{private:double _x1,_y1,_x2,_y2;public:Rectangle(Drawing *dp, double x1, double y1,double x2, double y2);void draw();};Rectangle::Rectangle(Drawing *dp, double x1, double y1, double x2, double y2):(5){_x1=x1;_y1=y1;_x2=x2;_y2=y2;}void Rectangle::draw(){//省略具体实现}
(18)如果一个直线控件在窗体上呈现为一条垂直线,则可以确定的是A)它的Yl、Y2属性的值相等B)它的X1、X2属性的值相等C)它的X1、Yl属性的值分别与X2, Y2属性的值相等D) 它的X1、X2属性的值分别与Y1、Y2属性的值相等
设配对设计资料的变量值为X1和x2(无差值为0者),则配对设计资料的符号秩和检验是A.分别按X1和X2从小到大编秩B.把X1和X2所有观察值混合从小到大编秩C.把X1和X2所有观察值混合按绝对值从小到大编秩D.把X1和X2的差值从小到大编秩E.把X1和X2的差值的绝对值从小到大编秩
设有两个参与人x和y,x有两个纯策略x1和x2,y有两个纯策略y1和y2。当y选择y1和y2时,x选择x1得到的支付分别为x11和x12,选择x2得到的支付分别为x1和x22;当x选择x1和x2时,y选择y1得到的支付分别为y11和y21,选择y2得到的支付分别为y12和y22 (1)试给出相应的博弈矩阵。 (2)这种博弈矩阵的表示是唯一的吗?为什么?
设f(x)处处连续,且在x=x1处有f'(x1)=0,在x=x2处不可导,那么( )。A.x=x1及x=x2都必不是f(x)的极值点B.只有x=x1是f(x)的极值点C.x=x1及x=x2都有可能是f(x)的极值点D.只有x=x2是f(x)的极值点
设配对资料的变量值为x1和x2,则配对资料的秩和检验()A、分别按x1和x2从小到大编秩B、把x1和x2综合从小到大编秩C、把x1和x2综合按绝对值从小到大编秩D、把x1和x2的差数按绝对值从小到大编秩
设配对设计资料的变量值为X1和X2,则配对资料的秩和检验()。A、把X1与X2的差数绝对值从小到大编秩B、把X1和X2综合从小到大编秩C、把X1和X2综合按绝对值从小到大编秩D、把X1与X2的差数从小到大编秩
设配对设计资料的变量值为X1和X2,则配对资料的秩和检验()A、分别按X1和X2从小到大编秩B、把X1和X2综合从小到大编秩C、把X1和X2综合按绝对值从小到大编秩D、把X1和X2的差数从小到大编秩E、把X1和X2的差数的绝对值从小到大编秩
已知X1=+0010100,Y1=+0100001,X2=0010100,Y2=0100001,试计算下列各式(设字长为8位)。 (1)[X1+Y1]补=[X1]补+[Y1]补=() (2)[X1-Y2]补=[X1]补+[-Y2]补=() (3)[X2-Y2]补=[X2]补+[-Y2]补=() (4)[X2+Y2]补=[X2]补+[Y2]补=()
设f(x)处处连续,且在x=x1处有f'(x1)=0,在x=x2处不可导,那么()。A、x=x1及x=x2都必不是f(x)的极值点B、只有x=x1是f(x)的极值点C、x=x1及x=x2都有可能是f(x)的极值点D、只有x=x2是f(x)的极值点
单选题设f(x)处处连续,且在x=x1处有f'(x1)=0,在x=x2处不可导,那么()。Ax=x1及x=x2都必不是f(x)的极值点B只有x=x1是f(x)的极值点Cx=x1及x=x2都有可能是f(x)的极值点D只有x=x2是f(x)的极值点
单选题如果一个直线控件在窗体上呈现为一条垂直线,则可以确定的是( )。A它的Y1、Y2属性的值相等B它的X1、X2属性的值相等C它的X1、Y1属性的值分别与X2、Y2属性的值相等D它的X1、X2属性的值分别与Y1、Y2属性的值相等
单选题使用Line控件在窗体上画一条从(0,0)到(600,700)的直线,则其相应属性的值应是( )。AX1=0,X2=600,Y1=0,Y2=700BY1=0,Y2=600,X1=0,X2=700CX1=0,X2=0,Y1=600,Y2=700DY1=0,Y2=0,X1=600,X2=700
单选题被测量Y与输入量X1、X2的估计值分别为y、x1和x2,它们之间的函数关系为y=x1+x2,且X1、X2之间不相关。若X1、X2的标准不确定度分别为:u1=10mg,u2=20mg,合成标准不确定度的有效自由度veff=4,假设被测量Y服从t分布,当包含概率为95%时,测得值的扩展不确定度是( )。A45mgB57mgC62mgD71mg
单选题若函数f(x)在区间(a,b)内可导,x1和x2是区间(a,b)内任意两点(x1<x2),则至少存在一点ξ,使( )Af(b)-f(a)=f′(ξ)(b-a)(a<ξ<b)Bf(b)-f(x1)=f′(ξ)(b-x1)(x1<ξ<b)Cf(x2)-f(x1)=f′(ξ)(x2-x1)(x1<ξ<x2)Df(x2)-f(a)=f′(ξ)(x2-a)(a<ξ<x2)
单选题已知被测量Y与输入量X1、X2、X3、X4、X5、的估计值分别为y、x1、x2、x3、x4、x5,它们之间的函数关系为y=x1+x2+x3+x4+x5,若输入量X1、X2、X3、X4、X5服从半宽度相同的均匀分布,且相互独立,则被测量Y在相应变化区间内接近( )分布。A正态B均匀C三角D反正弦
单选题设f(x)在(-∞,+∞)内可导,且对任意x2>x1,都有f(x2)>f(x1),则正确的结论是( )。A对任意x,f′(x)>0B对任意x,f′(x)≤0C函数-f(-x)单调增加D函数f(-x)单调增加
问答题设函数f(x)在(a,b)内连续,a<x1<x2<…<xn<b,证明:必∃ξ∈(a,b),使f(ξ)=[f(x1)+f(x2)+…+f(xn)]/n。