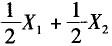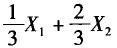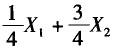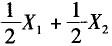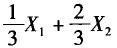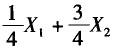对正态总体参数估计的描述正确的是( )。A.正态均值μ的无偏估计有两个,一个是样本均值的估计,另一个是样本中位数的估计,即μ(2=Me=(1/n)(X1+X2+…+Xn)B.对正态均值μ来说,样本均值总比样本中位数更有效,应舍去样本中位数C.在实际过程中,应优先选用样本均值去估计正态均值μ。但有时在现场,为了简便快捷,选用样本中位数去估计正态均值μ也是有的D.正态方差σ2的无偏估计常用的只有一个,就是样本方差S2
设X1,X2是来自N(μ,1)的样本,则()是总体均值μ的无偏估计。
设X1,X2,…,Xn是来自总体的样本,且EX=μ,DX=б2则()是μ的无偏估计。
设(X1,X2,…,Xn)是来自正态总体N(μ,σ2)的简单随机样本,其中参数μ,σ2未知,则下列各项中,不是统计量的有( )。
设X1,X2,…,Xn是来自正态总体N(μ,σ2)的一个样本,则有( )。
设X1,…,Xn是取自正态总体N(μ,1)的样本,其中μ未知,μ的无偏估计是( ).A.B.C.D.X-X1
设(X1,X2,…,Xn)(N≥2)为标准正态总体X的简单随机样本,则().
设(X1,X2,…,Xn)是抽自正态总体N(u,σ2)的一个容量为10的样本,
设总体X服从参数为λ的泊松分布,其中λ未知.X1,…,Xn是取自总体X的样本,则λ的最大似然估计是( ).A.B.C.SD.
从正态总体X~N(0,σ^2)中抽取简单随机样本X1,X2,…,Xn,则可作为参数σ^2的无偏估计量的是().
设X1,X2,…,Xn是来自正态总体N(μ,σ2)的一个样本,,s2分别是样本均值和样本方差,令,则有( )。A、W~t(n)B、W~t(n-1)C、W~F(n)D、W~F(n-1)
设X1,…,Xn是取自总体X的容量为n的样本,总体均值E(X)=μ未知,μ的无偏估计是( ).A.B.C.X1+XnD.
设总体X的概率密度为未知参数,X1,X2, ...Xn是来自总体X的样本,则θ的矩估计量是:
设总体X的概率密度为而x1,x2,...,xn 是来自总体的样本值,则未知参数θ的最大似然估计值是:
设总体X的概率密度为f(x)=其中θ>-1是未知参数,X1,X2,...Xn是来自总体X的样本,则θ的矩估计量是:
设总体X的分布函数为 其中未知参数β>1,X1,X2,…,Xn为来自总体X的简单随机样本,求: (Ⅰ)β的矩估计量;(Ⅱ)β的最大似然估计量.
设总体X的概率密度为f(x)=,其中θ>-1是未知参数,X1, X2,…,Xn是来自总体X的一个容量为n的简单随机样本,分别用矩估计法和最大似然估计法求参数θ的估计量.
设总体X的概率密度为其中θ是未知参数,X1,X2,…,Xn为来自总体X的简单随机样本.若是θ的无偏估计,则c=______.
设总体X的概率密度为 其中参数λ(λ>0)未知,X1,X2,…,Xn是来自总体X的简单随机样本.(Ⅰ)求参数λ的矩估计量;(Ⅱ)求参数λ的最大似然估计量.
设总体X的概率密度为 其中μ是已知参数,σ>0是未知参数,A是常数.X1,X2,…,Xn是来自总体X的简单随机样本. (Ⅰ)求A; (Ⅱ)求σ的最大似然估计量.
设总体X的概率密度为 其中θ为未知参数,X1,X2,…,Xn,为来自该总体的简单随机样本. (Ⅰ)求θ的矩估计量; (Ⅱ)求θ的最大似然估计量.
设总体X~N(0,σ2),X1,X2,...Xn是自总体的样本,则σ2的矩估计是:
设样本x1,x2,…,xn来自正态总体N(0,9),其样本方差为s2,则E(s2)=()
设总体X服从参数为λ的泊松分布,其中λ未知.X1,…,X是取自总体X的样本,则A的最大似然估计是().A、XB、S2C、SD、2
设X1,X2,…,Xn是从总体X中抽取的容量为n的一个样本,如果由此样本构造一个函数T(X1,X2,…,Xn),不依赖于任何未知参数,则函数T(X1,X2,…,Xn)是一个()
单选题设总体X服从参数为λ的泊松分布,其中λ未知.X1,…,X是取自总体X的样本,则A的最大似然估计是().AXBS2CSD2
问答题总体x~N(μ,σ2),x1,x2,…,xn为其样本,未知参数μ的矩估计为_______ .