设随机变量X～N（μ,σ^2）,其分布函数为F(x),则对任意常数a,有().A.F（a+μ）＋F(a－μ)=1B.F(μ+a)+F(μ－a)=1C.F（a）+F（-a）=1D.F(a－μ)~-F(μ-a)=1
设随机变量X～N（μ,σ^2）,其分布函数为F(x),则对任意常数a,有().
A.F（a+μ）＋F(a－μ)=1
B.F(μ+a)+F(μ－a)=1
C.F（a）+F（-a）=1
D.F(a－μ)~-F(μ-a)=1
B.F(μ+a)+F(μ－a)=1
C.F（a）+F（-a）=1
D.F(a－μ)~-F(μ-a)=1
参考解析
解析：因为X～N（μ，σ^2），所以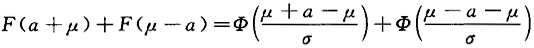
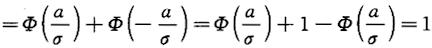，选(B).
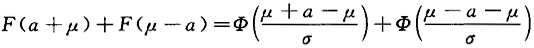
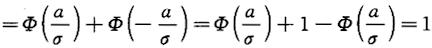，选(B).
相关考题：
正态分布计算所依据的重要性质为( )。A．设X～N(μ,σ2)，则u=(X-μ)/σ～N(0，1)B．设X～N(μ，σ2)，则对任意实数a、b有P(X＜b)=Ф[(b-μ)/σ)C．设X～N(μ，σ2)，则对任意实数a、b有P(X＞a)=1-Ф[(a-μ)/σ]D．设X～N(μ，σ2)，则对任意实数a、b有P(a＜X＜b)=Ф[(b-μ)/σ)-Ф[(a-μ)/σ]E．设X～μ(μ1，，Y～N(μ2，，则X+Y～N(μ1+μ2，(σ1+σ2) 2)
设连续型随机变量X的密度函数为f(x),分布函数为F(x).如果随机变量X与-X分布函数相同,则().A.F(z)=F（-x）B.F(x)=F（-x）C.F(X)=F（-x）D.f(x)=f（-x）
正态分布计算所依据的重要性质为（ ）。A.设X~N(μ,σ2),则μ= (X-μ)/σ~N(0, 1)B.设X~N(μ,σ2),则对任意实数a、b有P(XC.设X~N(μ,σ2),则对任意实数a、b有P(X>a) =1-Φ[(a-μ)/σ]D.设X~N(μ,σ2),则对任意实数a、b有P(a
设随机变量X，Y独立同分布，且X的分布函数为F(x)，则Z=max{X，Y}的分布函数为 A.AF^2(x)B.F(x)F(y)C.1-［1-F(x)］^2D.［1-F(x)］［1-F(y)］
设随机变量X的概率密度和分布函数分别是f（x）和F（x），且f（x）=f（-x），则对任意实数a，有F（-a）=（）A、1/2-F（a）B、1/2+F（a）C、2F（a）-1D、1-F（a）
设X1，X2是任意两个相互独立的连续型随机变量，它们的概率密度分别为f1（x）与f2（x），分布函数分别为F1（x）与F2（x），则（）A、f1（x）+f2（x）必为某一随机变量的概率密度B、f1（x）f2（x）必为某一随机变量的概率密度C、F1（x）+F2（x）必为某一随机变量的分布函数D、F1（x）F2（x）必为某一随机变量的分布函数
设F（x），G（x）是f（x）的两个原函数，则下面的结论不正确的是（）。A、F（x）+C也是f（x）的原函数，C为任意常数B、F（x）=G（x）+C，C为任意常数C、F（x）=G（x）+C，C为某个常数D、F’（x）=G’（x）
单选题设随机变量X，Y独立同分布，且X的分布函数为F（x），则Z＝max{X，Y}的分布函数为（ ）。AF2（x）BF（x）F（y）C1－[1－F（x）]2D[1－F（x）][1－F（y）]
单选题设X～N（2，22），其概率密度函数为f（x），分布函数F（x），则（ ）。AP{X≤0}＝P{X≥0}＝0.5Bf（－x）＝1－f（x）CF（x）＝－F（－x）DP{X≥2}＝P{X＜2}＝0.5
单选题设F（x），G（x）是f（x）的两个原函数，则下面的结论不正确的是（）。AF（x）+C也是f（x）的原函数，C为任意常数BF（x）=G（x）+C，C为任意常数CF（x）=G（x）+C，C为某个常数DF’（x）=G’（x）