设f(x)=dt,g(x)=x3+x4,当x→0时,f(x)是g(x)的().A.等价无穷小B.同阶但非等价无穷小C.高阶无穷小D.低阶无穷小
设f(x)=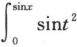
dt,g(x)=x3+x4,当x→0时,f(x)是g(x)的().
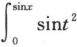dt,g(x)=x3+x4,当x→0时,f(x)是g(x)的().
A.等价无穷小
B.同阶但非等价无穷小
C.高阶无穷小
D.低阶无穷小
B.同阶但非等价无穷小
C.高阶无穷小
D.低阶无穷小
参考解析
解析：因为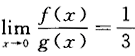
，所以正确答案为(B).
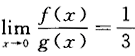，所以正确答案为(B).
相关考题：
设f(x),g(x),h(x)均为奇函数,则()中所给定的函数是偶函数。 A、f(x)g(x)h(x)B、[f(x)+g(x)]h(x)C、f(x)+g(x)D、f(x)+g(x)+h(x)
设函数f（x），g（x）在[a，b]上均可导（a＜b），且恒正，若f′（x）g（x）＋f（x）g′（x）＞0，则当x∈（a，b）时，下列不等式中成立的是（ ）。 A． [f（x）/g（x）]＞[f（a）/g（b）] B． [f（x）/g（x）]＞[f（b）/g（b）] C． f（x）g（x）＞f（a）g（a） D． f（x）g（x）＞f（b）g（b）
设函数f(x)具有二阶导数，g(x)=f(0)(1-x)+f(1)x，则在区间［0，1］上 A.A当f'(x)≥0时，f(x)≥g(x)B.当f'(x)≥0时，f(x)≤g(x)C.当f"(x)≥0时，f(x)≥g(x)D.当f"(x)≥0时，f(x)≤g(x)
设f(x)，g(x)在x=x0处均不连续，则在x=x0处( )A.f(x)+g(x)f(x)·g(X)均不连续B.f(x)+g(x)不连续,f(x)·g(x)的连续性不确定C.f(x)+g(x)的连续性不确定,f(x)·g(x)不连续D.f(x)+g(x)f(x)·g(x)的连续性均不确定
设函数f（x），g（x）是大于零的可导函数，且f′（x）g（x）-f（x）g′（x）＜0，则当a＜x＜b时有（ ）《》（ ）A.f（x）g（b）＞f（b）g（x）B.f（x）g（a）＞f（a）g（x）C.f（x）g（x）＞f（b）g（b）D.f（x）g（x）＞f（a）g（a）
设f（x），g（x）∈F[x]，若f（x）=0则有什么成立？（）A、deg（f（x）g（x））B、deg（f（x）g（x））＞max{degf（x），degg（x）}C、deg（f（x）+g（x））＞max{degf（x），degg（x）}D、deg（f（x）+g（x））=max{degf（x），degg（x）}
设F（x），G（x）是f（x）的两个原函数，则下面的结论不正确的是（）。A、F（x）+C也是f（x）的原函数，C为任意常数B、F（x）=G（x）+C，C为任意常数C、F（x）=G（x）+C，C为某个常数D、F’（x）=G’（x）
设K是个数域，K[x]中的多项式f（x），g（x），若有f=g，则可以得到什么？（）A、f（x）=g（f（x））B、g（x）=f（f（x））C、f（x）=g（x）D、g（x）=f（g（x））
设g（x），f（x）∈F[x]，存在d（x）∈F[x]，有d（x）|f（x）且d（x）|g（x），那么称d（x）为f（x），g（x）的什么？（）A、公因式B、最大公因式C、最小公因式D、共用函数
单选题设函数f（x），g（x）在[a，b]上均可导（a＜b），且恒正，若f′（x）g（x）＋f（x）g′（x）＞0，则当x∈（a，b）时，下列不等式中成立的是（ ）。[2018年真题]Af（x）/g（x）＞f（a）/g（b）Bf（x）/g（x）＞f（b）/g（b）Cf（x）g（x）＞f（a）g（a）Df（x）g（x）＞f（b）g（b）
问答题设函数f（x），g（x）二次可导，满足函数方程f（x）g（x）＝1，又f′（x）≠0，g′（x）≠0，则f″（x）/f′（x）－f′（x）/f（x）＝g″（x）/g′（x）－g′（x）/g（x）。