今有一倔强系数为k的轻弹簧,垂直放置,下端挂一质量为m的小球,使弹簧为原长而小球恰好与地而接触。今将弹簧上端缓慢地提起,直到小球刚能脱离地而为止,在这过程中外力所作的功为()。
今有一倔强系数为k的轻弹簧,垂直放置,下端挂一质量为m的小球,使弹簧为原长而小球恰好与地而接触。今将弹簧上端缓慢地提起,直到小球刚能脱离地而为止,在这过程中外力所作的功为()。
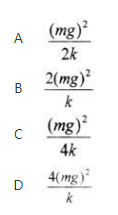
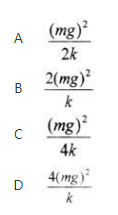
参考解析
解析:

相关考题:
如下图所示,一根轻弹簧下端固定,竖立在水平面上。其正上方A位置有一只小球。小球从静止开始下落,在B位置接触弹簧的上端.在C位置小球所受弹力大小等于重力,在D位置小球速度减小到零。下列对于小球下降阶段的说法中,正确的是______。A.在B位置小球动能最大B.在C位置小球动能最小C.从A→D位置小球重力势能的减少小于弹簧弹性势能的增加D.从A→C位置小球重力势能的减少大于小球动能的增加
图示在倾角为α的光滑斜面上置一弹性系数为k的弹簧,一质量为m的物块沿斜面下滑s距离与弹簧相碰,碰后弹簧与物块不分离并发生振动,则自由振动的固有圆频率应为:A. (k/m)1/2B.[k/(ms)]1/2C. [k/(msinα)]1/2D. (ksinα/m)1/2
.如图所示,在光滑桌面上有一轻质弹簧,它的两端连接质量不等的两个小球,用两手按小球,使弹簧被压缩而静止在桌面上,然后同时放手,在弹簧恢复原长的任意时刻,两小球的___-A.动能相等B.动量大小相等C.速度大小相等D.加速度大小相等
一质量为m的小球,从高出水面h处的A点自由落下,如图6所示。已知小球在水中受到的黏滞阻力与小球的运动速率v成正比(比例系数为k)。设小球在水中的浮力忽略不计,以小球恰好垂直落入水中时为计时起点(t=O)。求小球在水中的运动速率v与时间t的关系:
如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态,现缓慢向上提上面的木块,直到它刚离开上面弹簧,在这过程中下面木块移动的距离为( )。 A.B.C.D.
两个质量不同的质点用弹簧相连,平放在光滑的水平面上。弹簧刚度系数为k,弹簧原长为l0。现将两质点拉开,使弹簧拉长到l后无初速地释放。当弹簧恢复到原长瞬时:两个质点的速度都()。A、与k1/2成正比,与(l-l0)成正比B、与k成正比,与(l-l0)2成正比C、与k成正比,与(l-l0)成正比D、与k1/2成正比,与(l-l0)1/2成正比
电梯内的水平地板上,竖直放置一根轻质弹簧,弹簧上端固定质量为m的物体。当电梯沿竖直方向匀速运动时,弹簧被压缩了x;当电梯接着做减速运动时,弹簧又被继续压缩了0.1x。重力加速度大小为g。则弹簧的劲度系数k=();该电梯做匀速运动时的速度方向为(),电梯做减速运动时的加速度大小是()。
刘刚通过实验探究弹力与弹簧长度变化的关系,他应该得到的正确结论是:在发生弹性形变时,弹簧的弹力与弹簧的()成正比。实验中刘刚在弹簧下端悬挂50N重物时,弹簧长度为12cm,已知弹簧在弹性限度内,且弹簧原长为10cm,则他所用弹簧的劲度系数为()。
劲度系数为k的轻弹簧,竖直放置,下端悬挂一质量为m的小球,使弹簧为原长而小球恰好与地面接触,今将弹簧上端缓缓地提高直到小球刚好离开地面为止,在此过程中,外力所做的功为()。A、m2g2/2k B、m2g2/k C、m2g2/4k D、4m2g2/k
一个轻质弹簧竖直悬挂,原长为l,今将质量为m的物体挂在弹簧下端,同时用手托住重物缓慢放下,到达弹簧的平衡位置静止不动,在此过程中,系统的重力势能减少而弹性势能增加,则有()。A、减少的重力势能大于增加的弹性势能B、减少的重力势能等于增加的弹性势能C、减少的重力势能小于增加的弹性热能D、条件不足,无法确定
一根轻质弹簧,竖直悬挂,原长为10cm.当弹簧下端挂2.0N的重物时,伸长1.0cm;则当弹簧下端挂8.0N的重物时,弹簧的长度为()A、4.0cmB、14.0cmC、8.0cmD、18.0cm
单选题两个质量不同的质点用弹簧相连,平放在光滑的水平面上。弹簧刚度系数为k,弹簧原长为l0。现将两质点拉开,使弹簧拉长到l后无初速地释放。当弹簧恢复到原长瞬时:两个质点的速度都()。A与k1/2成正比,与(l-l0)成正比B与k成正比,与(l-l0)2成正比C与k成正比,与(l-l0)成正比D与k1/2成正比,与(l-l0)1/2成正比