如图,由四个全等的小长方形拼成一个大正方形,每个长方形的面积都是1,且长与宽之比大于等于2,则这个大正方形的面积至少为 ()。A.3B.4.5C.5D.5.5
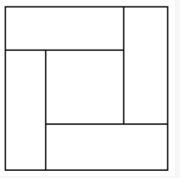
如图,由四个全等的小长方形拼成一个大正方形,每个长方形的面积都是1,且长与宽之比大于等于2,则这个大正方形的面积至少为 ()。

A.3
B.4.5
C.5
D.5.5
B.4.5
C.5
D.5.5
参考解析
解析:第一步,本题考查几何问题,属于其他几何类。
第二步,大正方形的面积=小长方形面积×4+中间小正方形的面积,由于每个长方形的面积都确定为1,那么要使大正方形的面积最小,则应使中间小正方形的面积最小。
第三步,设长方形的长为x,宽为y,则中间小正方形的边长为x-y,面积为(x-y)2,由条件可知x≥2y,那么当x=2y时,中间小正方形的面积(x-y)2最小,大正方形的面积也为最小。已知每个长方形的面积都为1,那么

第四步,大正方形的面积=

因此,选择B选项。
第二步,大正方形的面积=小长方形面积×4+中间小正方形的面积,由于每个长方形的面积都确定为1,那么要使大正方形的面积最小,则应使中间小正方形的面积最小。
第三步,设长方形的长为x,宽为y,则中间小正方形的边长为x-y,面积为(x-y)2,由条件可知x≥2y,那么当x=2y时,中间小正方形的面积(x-y)2最小,大正方形的面积也为最小。已知每个长方形的面积都为1,那么

第四步,大正方形的面积=

因此,选择B选项。
相关考题:
有四块小场地:第一块是边长a米的正方形,第二块是边长b米的正方形,其余两边都是长a米、宽b米的长方形。另有一块大长方形场地,它的面积等于上面四块场地面积的和,它的长为2(a+b)米,用最简单的式子表示出大长方形的宽
如图,甲、乙、丙、丁四个长方形拼成正方形 EFGH,中间阴影为正方形。已知,甲、乙、丙、丁四个长方形面积的和是 32cm2,四边形 ABCD 的面积是 20cm2。问甲、乙、丙、丁四个长方形周长的总和是( )。(图略)A.32cmB.56cmC.48cmD.68cm
如图所示,长方形ACEG被线段BF、HD分成四个大小不等的小长方形,已知AH等于6CM,GF等于3CM,DE等于10CM,BC等于7CM,则三角形ICG的面积为() A. 32НB. 28НC. 30НD. 26Н
如,正方形ABCD由四个相同的长方形和一个小正方形拼成,则能确定小正方形的面积(1)已知正方形ABCD的面积(2)已知长方形的长宽之比A.条件(1)充分,但条件(2)不充分B.条件(2)充分,但条件(1)不充分C.条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分D.条件(1)充分,条件(2)也充分E.条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
单选题船舶方型系数是指()。A设计水线面面积与长方形长×宽之比B设计水线下中剖面积与高×宽之比C设计水线下船体体积与长方形:长×宽×高的体积之比D设计水线面积与中横剖面面积之比