阅读以下函数说明和C代码，将C程序中(1)～(5)空缺处的内容补充完整。

【说明】

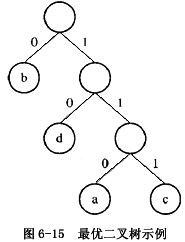
对给定的字符集合及相应的权值，采用哈夫曼算法构造最优二叉树，并用结构数组存储最优二叉树。例如，给定字符集合{a,b,c,d}及其权值2、7、4、5，可构造如图6-15所示的最优二叉树，以及相应的结构数组Ht(如表6-14所示，其中数组元素Ht[0]不用)。

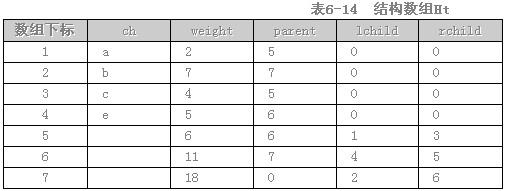
结构数组Ht的类型定义如下：

define MAXLEAFNUM 20

struct node{

char ch; /*扫当前节点表示的字符，对于非叶子节点，此域不用*/

Int weight； /*当前节点的权值*/

int parent; /*当前节点的父节点的下标，为0时表示无父节点*/

int lchild, rchild;

/*当前节点的左、右孩子节点的下标，为0时表示无对应的孩子节点*/

)Ht[2*MAXLEAFNUM];

用“0”或“广标识最优二叉树中分支的规则是：从一个节点进入其左(右)孩子节点，就用“0”(或“1”)标识该分支，如图6-15所示。

若用上述规则标识最优二叉树的每条分支后，从根节点开始到叶子节点为止，按经过分支的次序将相应标识依次排列，可得到由“0”、“1”组成的一个序列，称此序列为该叶子节点的前缀编码。例如，图6-15所示的叶子节点a、b、c、d的前缀编码分别是110、0、111、10。

函数void LeafCode(int root,int n)的功能是：采用非递归方法，遍历最优二叉树的全部叶子节点，为所有的叶子节点构造前缀编码。其中，形参root为最优二叉树的根节点下标；形参n为叶子节点个数。在函数void LeafCode(int root,int n)构造过程中，将Ht[p].weight域用做被遍历节点的遍历状态标志。

函数void Decode(char *buff,int root)的功能是：将前缀编码序列翻译成叶子节点的字符序列，并输出。其中，形参root为最优二叉树的根节点下标；形参buff指向前缀编码序列。

【函数4.1】

char **HC;

void LeafCode(int root, int n)

{ /*为最优二叉树中的n个叶子节点构造前缀编码，root是树的根节点下标*/

int I,p=root,cdlen=0;

char code[20];

Hc = (char **)malloc((n+1)*sizeof(char *)); /*申请字符指针数组*/

For(i = 1;i＜= p;++I)

Ht [i]. weight = 0; /*遍历最优二叉树时用做被遍历节点的状态标志* /

While (p) { /*以非递归方法遍历最优二叉树，求树中每个叶子节点的编码*/

If(Ht[p].weight == 0) { /*向左*/

Ht[p].weight = 1;

If(Ht[p].lchild != 0) {

p = Ht[p].lchild;

code[cdlen++] = '0';

}

else if(Ht[p].rchild == 0) { /*若是叶子节点,则保存其前缀编码*/

Hc[p] = (char *)malloc((cdlen+1)*sizeof(char));

(1);

strcpy (Hc [p],code);

}

}

else if(Ht[p].weight == 1) { /*向右*/

Ht [p].weight = 2;

If(Ht[p].rchild != 0) {

p = Ht [p].rchild;

code[cdlen++] ='1';

}

}

else { /*Ht[p].weight == 2,回退/

Ht [p].weight = 0;

p =(2);

(3); /*退回父节点*/

}

} / *while .结束* /

}

【函数4.2】

void Decode(char *buff,int root)

{ int pre = root,p;

while(*buff != '\0') {

p = root;

&