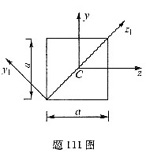
如图所示正方形截面对z1轴的惯性矩与对z轴的惯性矩的关系为( )。
如图所示正方形截面对z1轴的惯性矩与对z轴的惯性矩的关系为( )。



参考解析
解析:正方形截面的任何一条形心轴均为形心主轴,其形心主惯性矩都相等
相关考题:
已知平面图形的形心为C,面积为A,对Z轴的惯性矩为IZ,则图形对Z1轴的惯性矩为( )。A.IZ+B.2A.B.IZ+(A.+B.)2A.C.IZ+(A.2-B.2)A.D.IZ+(B.2-A.2)A.
如图5-17所示,已知平面图形的形心为C,面积为A,对z轴的惯性矩为Iz,对图形z1轴的惯性矩有四种答案为( )。A. Iz + b2A B. Iz +(a + b)2 AC. Iz + (a2 -b2)A D. Iz+(b2 -a2)A
截面对任一轴的惯性矩等于它对平行于该轴的形心轴的惯性矩加上截面与两轴间距离的()与()的乘积。