已知某垄断厂商的短期总成本函数为STC =0. 1Q3 -6Q2+140Q +3000,反需求函数为P=150 -3. 25Q.
已知某垄断厂商的短期总成本函数为STC =0. 1Q3 -6Q2+140Q +3000,反需求函数为P=150 -3. 25Q.
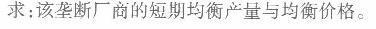
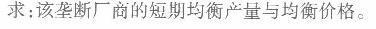
参考解析
解析: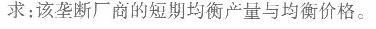
于是,根据垄断厂商短期利润最大化的原则MR= SMC,有: 0. 3Q2 _12Q +140 =150 -6. 5Q, 整理得3Q2—55Q -100 =0,解得Q=20(负值舍去)。 以Q =20代入反需求函数,得P=150 -3. 25Q =150 -3. 25×20= 85。 所以,该垄断厂商的短期均衡产量为Q= 20,均衡价格为P=85。
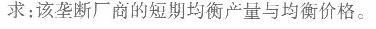
于是,根据垄断厂商短期利润最大化的原则MR= SMC,有: 0. 3Q2 _12Q +140 =150 -6. 5Q, 整理得3Q2—55Q -100 =0,解得Q=20(负值舍去)。 以Q =20代入反需求函数,得P=150 -3. 25Q =150 -3. 25×20= 85。 所以,该垄断厂商的短期均衡产量为Q= 20,均衡价格为P=85。
相关考题:
计算题:已知某完全竞争行业中的单个厂商的短期成本函数为STC=0.1Q3-2Q2+15Q+10。试求: 计算题:已知某完全竞争行业中的单个厂商的短期成本函数为STC=0.1Q3-2Q2+15Q+10。试求:(1)当市场上产品的价格为P=55时,厂商的短期均衡产量和利润;(2)当市场上价格下降为多少时,厂商必须停产;(3)厂商的短期供给函数
已知某个完全竞争行业中的单个厂商的短期成本函数是STC=0.1Q3—2Q2+15Q+10。求:(1)当市场上产品的价格为P=55时,厂商的短期均衡产量和利润;(2)当市场价格下降为多少时,厂商必须停产;(3)厂商的短期供给函数。
假定某完全竞争行业有100个相同的厂商,单个厂商的短期总成本函数为.STC=Q2+6Q +20。 (l)求市场的短期供给函数。 (2)假定市场的需求函数为Qd=420 - 30P,求该市场的短期均衡价格和均衡产量。 (3)假定政府对每一单位商品征收1.6元的销售税,那么,该市场的短期均衡价格和均衡产量是多少?消费者和厂商各自负担多少税收?
假定某寡头厂商面临一条弯折的需求曲线,产量在0~30单位范围内时需求函数为P=60-0.3Q,产量超过30单位时需求函数为P=66 -0.50;该厂商的短期总成本函数为STC=0.005 Q3-0. 2Q2 +36Q +200。 (1)求该寡头厂商利润最大化的均衡产量和均衡价格。 (2)假定该厂商成本增加,导致短期总成本函数变为STC =0.005Q3 -0.2Q2 +50Q +200,求该寡头厂商利润最大化的均衡产量和均衡价格。 (3)对以上(1)和(2)的结果作出解释。
已知某完全竞争行业中的单个厂商的短期成本函数为STC =0.1Q3- 2Q2+150 +10 . (1)求当市场上产品的价格为P=55时,厂商的短期均衡产量和利润。 (2)当市场价格下降为多少时,厂商必须停产? (3)求厂商的短期供给函数。
已知某垄断厂商的短期总成本函数为STC =0. 6Q2+3Q +2,反需求函数为P=8 -0. 4Q: (1)求该厂商实现利润最大化时的产量、价格、收益和利润。 (2)求该厂商实现收益最大化时的产量、价格、收益和利润。 (3)比较(1)和(2)的结果。
假设某完全竞争行业有200个相同的企业,企业的短期成本函数为TC =0. 2Q2+Q+15,市场需求函数为Qp= 2475 - 95P,厂商的长期总成本函数为LTC=0.1Q3-1. 2Q2+11.1Q,求: (1)市场短期均衡价格、产量及厂商利润。 (2)市场长期均衡价格与产量。 (3)说明是否会有厂商退出经营。
已知某完全竞争市场的需求函数为D= 6300 - 400P,短期市场供给函数为SS= 3000+150P;单个企业在LAC曲线最低点的价格为6,产量为50;单个企业的成本规模不变. (1)求市场的短期均衡价格和均衡产量。 (2)判断(1)中的市场是否同时处于长期均衡,求行业内的厂商数量: (3)如果市场的需求函数变为D’=8000 - 400P,短期供给函数为SS’= 4700 +150P,求市场的短期均衡价格和均衡产量。 (4)判断(3)中的市场是否同时处于长期均衡,并求行业内的厂商数量。 (5)判断该行业属于什么类型。 (6)需要新加入多少企业,才能提供由(1)到(3)所增加的行业总产量?
已知某完全竞争行业中的单个厂商的短期成本函数为STC=0.1Q3—2Q2+15Q+10。试求:(1)当市场上产品的价格为P=55时,厂商的短期均衡产量和利润;(2)当市场价格下降为多少时,厂商必须停产;(3)厂商的短期供给函数。
问答题计算题: 已知某完全竞争行业中的单个厂商的短期成本函数为STC=0.1Q3-2Q2+15Q+10。试求: (1)当市场上产品的价格为P=55时,厂商的短期均衡产量和利润; (2)当市场上价格下降为多少时,厂商必须停产; (3)厂商的短期供给函数
问答题已知完全竞争市场的需求函数为D=6300-400P,短期市场供给函数为SS=3000+150P,单个企业在LAC曲线最低点的价格为6,产量为50,单个企业的成本规模不变。 求:(1)市场短期均衡价格与均衡产量。 (2)判断该市场是否同时处于长期均衡,求行业内的厂商数量。 (3)如果市场的需求函数变为D′=8000-400P,短期供给函数SS′=4700+150P,求市场短期均衡的价格和产量。 (4)判断该市场是否同时处于长期均衡,并求行业内厂商数量。
问答题某垄断厂商的反需求函数为P=150-3Q,成本函数为TC=15Q+0.5Q2。 (1)计算利润最大化的价格和产出。 (2)如果厂商追求销售收入最大化,其价格和产出又如何? (3)政府决定价格不准高于40元,该厂商的产量为多少?会造成过剩还是短缺?
问答题已知某完全竞争行业中的单个厂商的短期成本函数为STC=0.1Q3—2Q2+15Q+10。试求:(1)当市场上产品的价格为P=55时,厂商的短期均衡产量和利润;(2)当市场价格下降为多少时,厂商必须停产;(3)厂商的短期供给函数。
问答题已知某完全竞争行业中的单个厂商的短期成本函数为:STC=0.1Q3-2Q2+15Q+10(1)当市场上产品价格为 55时厂商的短期均衡产量和利润;(2)当市场价格下降为多少时厂商必须停产?(3)求厂商的短期供给函数。