用最小二乘法拟合回归直线方程,其基本原理是( )。
用最小二乘法拟合回归直线方程,其基本原理是( )。
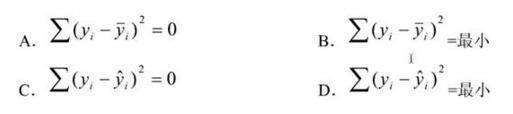
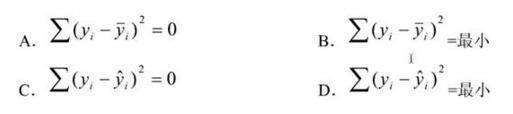
参考解析
解析:
相关考题:
用最小二乘法以利润率为因变量拟合直线回归方程,其最小二乘法的原理是使( )。A.实际Y值与理论 值的离差和最小B.实际Y值与理论 值的离差平方和最小C.实际Y值与Y平均值的离差和最小D.实际Y值与Y平均值的离差平方和最小
直线回归分析中,对回归系数做假设检验的目的是 A、检验回归系数b是否等于0B、检验两总体回归系数是否相等C、检验回归方程的拟合优度D、推断两变量是否存在直线依存关系E、判断回归方程代表性的好坏
根据最小二乘法拟合的趋势回归方程为:Tt= 112.67+0.698t,R2=0.944,说明( )。A.该回归方程的拟合效果较好B.该回归方程的拟合效果较差C.该方程对变量的解释程度为94.4%D.时间每增加一个单位,T增加0.698个单位E.时间每增加一个单位,T平均增加0.698个单位
用最小二乘法以利润率为因变量拟合直线回归方程,其最小二乘法的原理是使( )。A.实际Y值与理论Y值的离差和最小B.实际Y值与理论Y值的离差平方和最小C.实际Y值与Y平均值的离差和最小D.实际Y值与Y平均值的离差平方和最小
用最小二乘法确定直线回归方程的原则是A.各观测点距回归直线的纵向距离相等B.各观测点距回归直线的纵向距离平方和最小C.各观测点距回归直线的垂直距离相等D.各观测点距回归直线的垂直距离平方和最小E.各观测点距回归直线的纵向距离最小
关于一元线性回归的正确表述有( )。A.用来计算相关系数B.是描述两个变量之间相关关系的最简单的回归模型C.只涉及一个自变量D.使用最小二乘法确定一元线性回归方程的系数E.用决定系数来测度回归直线对样本数据的拟合程度
单选题直线回归分析中,对回归系数做假设检验的目的是()。A检验回归系数b是否等于0B检验两总体回归系数是否相等C检验回归方程的拟合优度D推断两变量是否存在直线依存关系E判断回归方程代表性的好坏
单选题评价回归直线方程拟合优度如何的指标有()A回归系数bB直线截距aC判定系数r2D相关系数r