假设某公司股票目前的市场价格为45元,6个月后的价格可能是55元和35元两种情况。有1股以该股票为标的资产的看涨期权,到期时间是6个月,执行价格为48元。投资者可以购进上述股票且按无风险利率10%借入资金,同时售出一份该股票的看涨期权。则套期保值比率为( )。A、0.35B、0.2C、0.1D、0.5
假设某公司股票目前的市场价格为45元,6个月后的价格可能是55元和35元两种情况。有1股以该股票为标的资产的看涨期权,到期时间是6个月,执行价格为48元。投资者可以购进上述股票且按无风险利率10%借入资金,同时售出一份该股票的看涨期权。则套期保值比率为( )。
A、0.35
B、0.2
C、0.1
D、0.5
B、0.2
C、0.1
D、0.5
参考解析
解析:套期保值比率=
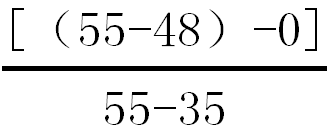
=0.35。
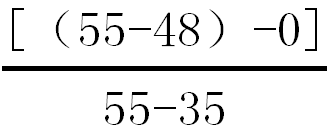
=0.35。
相关考题:
假设ABC公司股票目前的市场价格为50元,而在一年后的价格可能是60元和40元两种情况。再假定存在一份100股该种股票的看涨期权,期限是一年,执行价格为50元。投资者可以按l0%的无风险利率借款。购进上述股票且按无风险利率10%借人资金,同时售出一份100股该股票的看涨期权。则按照复制原理,下列说法正确的有( )。 A.购买股票的数量为50股 B.借款的金额是1818元 C.期权的价值为682元 D.期权的价值为844元
假设某公司股票目前的市场价格为25元,而在6个月后的价格可能是32元和18元两种情况。再假定存在一份l00股该种股票的看涨期权,期限是半年,执行价格为28元。投资者可以按10%的无风险年利率借款。购进上述股票且按无风险年利率10%借入资金,同时售出一份100股该股票的看涨期权。 要求: (1)根据单期二叉树期权定价模型,计算一份该股票的看涨期权的价值; (2)假设股票目前的市场价格、期权执行价格和无风险年利率均保持不变,若把6个月的时间分为两期,每期3个月,若该股票收益率的标准差为0.35,计算每期股价上升百分比和股价下降百分比; (3)结合(2),分别根据套期保值原理、风险中性原理和两期二叉树期权定价模型,计算一份该股票的看涨期权的价值。
假设ABC公司股票目前的市场价格为45元,而在一年后的价格可能是58元和42元两种情况。再假设存在一份200股该种股票的看涨期权,期限是一年,执行价格为48元。投资者可以按10%的无风险利率借款。购进上述股票且按无风险利率10%借入资金,同时售出一份200股该股票的看涨期权,则套期保值比率为( )。A.125B.140C.220D.156
假设ABC公司股票目前的市场价格为28元,而在6个月后的价格可能是40元和20元两种情况。再假定存在一份100股该种股票的看涨期权,期限是半年,执行价格为28元。投资者可以按10%的无风险年利率借款。购进上述股票且按无风险年利率10%借入资金,同时售出一份100股该股票的看涨期权。要求:(1)根据单期二叉树期权定价模型,计算一份该股票的看涨期权的价值。(2)假设股票目前的市场价格、期权执行价格和无风险年利率均保持不变,若把6个月的时间分为两期,每期3个月,若该股票收益率的标准差为0.08,计算每期股价上升百分比和股价下降百分比。(3)结合(2)分别根据套期保值原理和风险中性原理,计算一份该股票的看涨期权的价值。
假设ABC公司股票目前的市场价格为24元,而在一年后的价格可能是35元和16元两种情况。再假定存在一份100股该种股票的看涨期权,期限是一年,执行价格为30元。投资者可以按10%的无风险利率借款。购进上述股票且按无风险利率10%借入资金,同时售出一份100股该股票的看涨期权。要求:(1)根据套期保值原理,计算套期保值比率、按无风险利率借入资金的数额以及一份该股票的看涨期权的价值。(2)根据风险中性原理,计算一份该股票的看涨期权的价值。(3)若目前一份100股该股票看涨期权的市场价格为306元,按上述组合投资者能否获利。
甲公司股票当前每股市价为80元,6个月以后,股价有两种可能:上升25%或下降20%。市场上有两种以该股票为标的资产的期权:看涨期权和看跌期权。每份看涨期权可买入1股股票,每份看跌期权可卖出1股股票;两种期权执行价格均为85元,到期时间均为6个月;期权到期前,甲公司不派发现金股利,年无风险利率为6%。要求:?、利用套期保值原理,计算看涨期权的股价上行时到期日价值、套期保值比率及期权价值,利用看涨期权—看跌期权平价定理,计算看跌期权的期权价值。?、假设市场上每份看涨期权价格6.5元,每份看跌期权价格8.5元,投资者同时卖出一份看涨期权和一份看跌期权,计算确保该组合不亏损的股票价格区间;如果6个月后的标的股票价格实际上涨20%,计算该组合的净损益。(注:计算股票价格区间和组合净损益时,均不考虑期权价格的货币时间价值)。
假设C公司股票现在的市价为20元,有1股以该股票为标的资产的看涨期权,执行价格为15元,到期时间是6个月。6个月后股价有两种可能:上升25%或者降低20%,无风险报酬率为每年6%。现在打算购进适量的股票以及借入必要的款项建立一个投资组合,使得该组合6个月后的价值与购进该看涨期权相等。<1>、确定可能的到期日股票价格;<2>、根据执行价格计算确定期权到期日价值;<3>、计算套期保值比率;<4>、计算购进股票的数量和借款数额;<5>、根据上述计算结果计算期权价值;<6>、根据风险中性原理计算期权的现值(假设股票不派发红利)。
假设该公司的股票现在市价为45元。有1股以该股票为标的资产的看涨期权,执行价格为48元,到期时间是6个月。6个月以后股价有两种可能:上升33.33%,或者下降25%,年无风险报价利率为4%,则利用复制原理确定期权价格时,下列说法错误的有( )。A.股价上行时期权到期日价值12元B.套期保值比率为0.8C.购买股票支出20.57元D.以无风险利率借入14元
假设甲公司股票现在的市价为10元,有1股以该股票为标的资产的看涨期权,执行价格为12元,到期时间是9个月。9个月后股价有两种可能:上升25%或者降低20%,无风险利率为每年6%。现在打算购进适量的股票以及借入必要的款项建立一个投资组合,使得该组合9个月后的价值与购进该看涨期权相等。 要求:(1)确定可能的到期日股票价格;(2)根据执行价格计算确定到期日期权价值;(3)计算套期保值比率;(4)计算购进股票的数量和借款数额;(5)计算期权的价值。
某公司股票目前的市价为40元,有1份以该股票为标的资产的欧式看涨期权(1份期权包含1股标的股票),执行价格为42元,到期时间为6个月。6个月以后股价有两种可能:上升20%或者下降25%,则套期保值比率为( )。A.0.33B.0.26C.0.42D.0.28
假设ABC公司股票目前的市场价格为24元,而在一年后的价格可能是36元和16元两种情况。市场上有两种以该股票为标的资产的期权:看涨期权和看跌期权。每份看涨期权可以买入1股股票,每份看跌期权可卖出1股股票,两种期权执行价格均为30元,到期时间为一年,一年以内公司不会派发股利,无风险利率为每年10%。要求:(1)根据复制原理,计算一份该股票的看涨期权的价值,利用看涨期权-看跌期权平价定理,计算看跌期权的价值。(2)若目前一份该股票看涨期权的市场价格为3.6元,能否创建投资组合进行套利,如果能,应该如何创建该组合。
甲公司股票当前每股市价为50元,6个月以后,股价有两种可能:上升20%或下降17%。市场上有两种以该股票为标的资产的期权:看涨期权和看跌期权。每份看涨期权可买1股股票,每份看跌期权可卖出1股股票;两种期权执行价格均为55元,到期时间均为6个月;期权到期前,甲公司不派发现金股利,半年无风险报酬率为2.5%。 要求: (1)利用套期保值原理,计算看涨期权的股价上行时到期日价值、套期保值比率及期权价值,利用看涨期权—看跌期权平价定理,计算看跌期权的期权价值。 (2)假设目前市场上每份看涨期权价格为2.5元,每份看跌期权价格为6.5元,投资者同时买入1份看涨期权和1份看跌期权,计算确保该组合不亏损的股票价格区间;如果6个月后,标的股票价格实际下降10%,计算该组合的净损益。(注:计算股票价格区间和组合净损益时,均不考虑期权价格的货币时间价值。)
假设ABC 公司的股票现在的市价为80 元。有1 股以该股票为标的资产的看涨期权,执行价格为85 元,到期时间6 个月。6 个月以后股价有两种可能:上升33.33%,或者降低25%。无风险报酬率为每年4%。则使用套期保值原理估算出该看涨期权价值为( )元。A.21.664B.37.144C.27.31D.9.834
假设C公司股票现在的市价为20元,有1股以该股票为标的资产的看涨期权,执行价格为15元,到期时间是6个月。6个月后股价有两种可能:上升25%或者降低20%,无风险利率为每年6%。现在打算购进适量的股票以及借入必要的款项建立一个投资组合,使得该组合6个月后的价值与购进该看涨期权相等。 (1)确定可能的到期日股票价格; (2)根据执行价格计算确定期权到期日价值; (3)计算套期保值比率; (4)计算购进股票的数量和借款数额; (5)根据上述计算结果计算期权价值; (6)根据风险中性原理计算期权的现值(假设股票不派发红利)。
某股票的现行价格为20 元,以该股票为标的资产的欧式看涨期权和欧式看跌期权的执行价格均为24.96 元,都在6 个月后到期。年无风险利率为8%,如果看涨期权的价格为10 元,看跌期权的价格应为( )元。A.6B.6.89C.13.11D.14
假设甲公司股票现在的市价为8元,有1股以该股票为标的资产的看涨期权,执行价格为9元,到期时间是9个月。9个月后股价有两种可能:上升30%或者降低10%,无风险利率为每年4%。现在打算购进适量的股票以及借入必要的款项建立一个投资组合,使得该组合9个月后的价值与购进该看涨期权相等。 要求:(结果均保留两位小数) (1)确定可能的到期日股票价格; (2)根据执行价格计算确定到期日期权价值; (3)计算套期保值率; (4)计算购进股票的数量和借款数额; (5)根据上述计算结果计算期权价值。
假设某公司股票目前的市场价格为49.5元,而一年后的价格可能是61.875元和39.6元两种情况。再假定存在一份200股该种股票的看涨期权,期限是一年,执行价格为52.8元。投资者可以购进上述股票且按无风险报价利率10%借入资金,同时售出一份200股该股票的看涨期权。则套期保值比率为( )。 A.81.48 B.91.48 C.125 D.156
假设C公司股票现在的每股市价为10元,有1股以该股票为标的资产的看涨期权,执行价格为6元,到期时间为6个月。6个月后股价有两种可能:上升25%或者降低20%,无风险利率为每年4%。现在打算购进适量的股票以及借入必要的款项建立一个投资组合,使得该组合6个月后的价值与购进该看涨期权相等。要求:(1)确定可能的到期日股票价格。(2)根据执行价格计算确定期权到期日价值。(3)计算套期保值比率。(4)计算购进股票的数量和借款数额。(5)根据上述结果计算期权价值。(6)如果该看涨期权的现行价格为6.12元,请根据套利原理,构建一个投资组合进行套利,并计算获利金额。
ABC公司的股票目前的股价为10元,有1股以该股票为标的资产的欧式看涨期权,执行价格为10元,期权价格为2元,到期时间为6个月。假设年无风险利率为4%,计算1股以该股票为标的资产、执行价格为10元、到期时间为6个月的欧式看跌期权的价格;
问答题ABC公司的股票目前的股价为10元,有1股以该股票为标的资产的欧式看涨期权,执行价格为10元,期权价格为2元,到期时间为6个月。假设年无风险利率为4%,计算1股以该股票为标的资产、执行价格为10元、到期时间为6个月的欧式看跌期权的价格;
单选题某股票的现行价格为20元,以该股票为标的资产的欧式看涨期权和欧式看跌期权的执行价格均为24.96。都在6个月后到期。年无风险利率为8%,如果看涨期权的价格为10元,看跌期权的价格为()元。A6.89B13.11C14D6
问答题计算分析题:假设C公司股票现在的市价为20元,有1股以该股票为标的资产的看涨期权,执行价格为15元,到期时间为6个月。6个月后股价有两种可能:上升25%或者降低20%,无风险利率为每年6%。现在打算购进适量的股票以及借入必要的款项建立一个投资组合,使得该组合6个月后的价值与购进该看涨期权相等。要求:(1)确定可能的到期日股票价格;(2)根据执行价格计算确定期权到期日价值;(3)计算套期保值比率;(4)计算购进股票的数量和借款数额;(5)根据上述计算结果计算期权价值;(6)根据风险中性原理计算期权的现值(假设期权期限内标的股票不派发红利)。
单选题假设ABC公司股票目前的市场价格50元,而在一年后的价格可能是60元或40元两种情况。再假定存在一份100股该种股票的看涨期权,期限是一年,执行价格为50元。投资者可以按10%的无风险利率借款。购进上述股票且按无风险利率10%借入资金,同时售出一份100股该股票的看涨期权。则按照复制原理,下列说法错误的是()。A购买股票的数量为50股B借款的金额是1818元C期权的价值为682元D期权的价值为844元
问答题假设ABC公司的股票现在的市价为30元。有1份以该股票为标的资产的看涨期权,执行价格为30.5元,到期时间是6个月。6个月以后股价有两种可能:上升35%,或者下降20%。无风险利率为每年4%。拟利用复制原理,建立一个投资组合,包括购进适量的股票以及借入必要的款项,使得该组合6个月后的价值与购进该看涨期权相等。期权的价值为多少?
问答题甲公司股票当前每股市价为50元,6个月后,股价有两张可能:上市20%或下降17%。市场上有两种以该股票为标的资产的期权:看涨期权和看跌期权。每份看涨期权可买1股股票,每份看跌期权可卖出1股股票;两张期权执行价格均为55元,到期时间均为6个月;期权到期前,甲公司不派发现金股利,半年无风险报酬率为2. 5%。要求:(1)利用套期保值原理,计算甲公司的套期保值比率H、借款数额日、期权价值。(2)假设目前市场上每份看涨期权价格为3元,每份看跌期权价格为5.5元,投资者同时买入1份看涨期权和1份看跌期权,计算确保该组合不亏损的股票价格区间;如果6个月后,标的股票价格实际上升10%,计算该组合的净损益。(注:计算股票价格区间和组合净损益时,均不考虑期权价格的货币时间价值)
问答题假设甲公司股票现在的市价为10元,有1股以该股票为标的资产的看涨期权,执行价格为6元,到期时间是9个月。9个月后股价有两种可能:上升25%或者降低20%,无风险利率为每年6%。现在打算购进适量的股票以及借入必要的款项建立一个投资组合,使得该组合9个月后的价值与购进该看涨期权相等。 要求: (1)确定可能的到期日股票价格; (2)根据执行价格计算确定到期日期权价值; (3)计算套期保值比率; (4)计算购进股票的数量和借款数额; (5)根据上述计算结果计算期权价值; (6)根据风险中性原理计算期权的现值(假设股票不派发红利)。
单选题假设某公司股票目前的市场价格为20元,半年后股价有两种可能:上升33.33%或者降低25%。现有1股以该股票为标的资产的看涨期权,执行价格为23元,到期时间为6个月,则套期保值比率为( )。A0.31B0.38C0.46D0.57