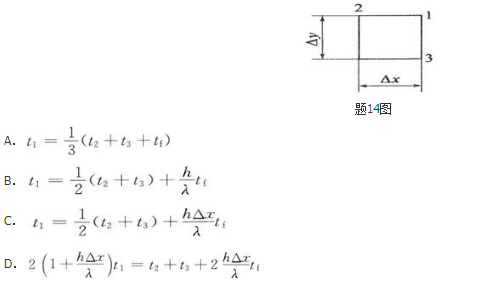
常物性无内热源二维稳态导热过程,在均匀网格步长下,Δx=Δy如图所示的拐角节点1处于第三类边界条件时,其差分格式为( )。
常物性无内热源二维稳态导热过程,在均匀网格步长下,Δx=Δy如图所示的拐角节点1处于第三类边界条件时,其差分格式为( )。

参考解析
解析:第三类边界条件:已知壁面相邻流体温度和表面传热系数。本题图示拐角节点1所代表的微元体为四分之一网格,由热平衡关系式列节点1的平衡方程:
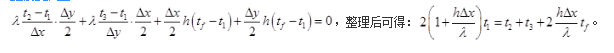
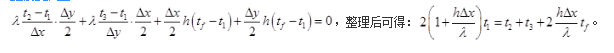
相关考题:
物性参数为常数的一圆柱导线,通过的电流均匀发热,导线与空气间的表面传热系数为定值,建立导线的导热微分方程采用()。 A、柱坐标下一维无内热源的不稳态导热微分热方程B、柱坐标下一维无内热源的稳态导热微分热方程C、柱坐标下一维有内热源的不稳态导热微分热方程D、柱坐标下一维有内热源的稳态导热微分热方程
常物性有内热源(qc=C,W/m3)二维稳态导热过程,在均匀网格步长下,如图所示,其内节点差分方程可写为( )。A. tp=(t1+t2+t3+qv/λ)/4B. tp=(t1+t2+t3+t4)/4+qvΔx2/(4λ)C. tp=(t1+t2+t3+t4)/4+qvΔx2D. tp=(t1+t2+t3+t4)/4
在稳态常物性无内热源的导热过程中,可以得出与导热率(导热系数)无关的温度分布通解,t=ax+b,其具有特性为( )。 A. 温度梯度与热导率成反比B. 导热过程与材料传导性能无关C. 热量计算也与热导率无关D. 边界条件不受物理性质影响
物性参数为常数的一圆柱导线,通过的电流均匀发热,导线与空气间的表面传热系数为定值,建立导线的导热微分方程采用( )。A.柱坐标下一维无内热源的不稳态导热微分方程B.柱坐标下一维无内热源的稳态导热微分方程C.柱坐标下一维有内热源的不稳态导热微分方程D.柱坐标下一维有内热源的稳态导热微分方程
对于二维稳态导热过程,如果物性参数为常数,t1、t2、t3和t4分别为四周四点温度,t5为中心节点温度,则均匀网格有限差分的内部节点方程()A、t1+t2+t3+t4-t5=0;B、t1+t2+t3+t4-4t5=0;C、t1+t2+t3+t4-6t5=0;D、t1+t2+t3+t4-2t5=0
对于矩形区域内的常物性,无内热源的导热问题,试分析在下列四种边界条件的组合下,导热物体为铜或钢时,物体中的温度分布是否一样: (1)四边均为给定温度; (2)四边中有一个边绝热,其余三个边均为给定温度; (3)四边中有一个边为给定热流(不等于零),其余三个边中至少有一个边为给定温度; (4)四边中有一个边为第三类边界条件。
单选题在稳态常物性无内热源的导热过程中,可以得出与导热率(导热系数)无关的温度分布通解,t=ax+b,其具有特性为( )。[2018年真题]A温度梯度与热导率成反比B导热过程与材料传导性能无关C热量计算也与热导率无关D边界条件不受物理性质影响
单选题常物性无内热源一维非稳态导热过程第三类边界条件下可微分得到离散方程,进行计算时要达到收敛需满足( )。[2011年真题]ABi<1/2BFo≤1CFo≤[1/(2Bi+2)]DFo≤1/(2Bi)
问答题有人对二维矩形物体中的稳态无内热源常物性的导热问题进行了数值计算。矩形的一个边绝热,其余三个边均与温度为tf的流体发生对流换热。你能预测他所得的温度场的解吗?