根据抽样调查数据对人均消费和人均可支配收入进行回归分析,得到估计的一元线性回归模型Y=1000+0.7X(X:人均可支配收入,Y:人均消费;单位均为元)。关于该回归模型的说法,正确的有()。A.人均可支配收入每增加1元,人均消费将平均增长0.7元B.人均可支配收入每减少1元,人均消费将平均增长0.7元C.人均可支配收入每增加1%,人均消费将平均增长0.7%D.人均可支配收入每减少1%,人均消费将平均增长0.7%E.当人均可支配收入为20000元时,人均消费将为15000元
根据抽样调查数据对人均消费和人均可支配收入进行回归分析,得到估计的一元线性回归模型Y=1000+0.7X(X:人均可支配收入,Y:人均消费;单位均为元)。关于该回归模型的说法,正确的有()。
A.人均可支配收入每增加1元,人均消费将平均增长0.7元
B.人均可支配收入每减少1元,人均消费将平均增长0.7元
C.人均可支配收入每增加1%,人均消费将平均增长0.7%
D.人均可支配收入每减少1%,人均消费将平均增长0.7%
E.当人均可支配收入为20000元时,人均消费将为15000元
B.人均可支配收入每减少1元,人均消费将平均增长0.7元
C.人均可支配收入每增加1%,人均消费将平均增长0.7%
D.人均可支配收入每减少1%,人均消费将平均增长0.7%
E.当人均可支配收入为20000元时,人均消费将为15000元
参考解析
解析: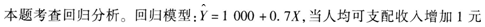
时,人均消费增加=1000+0.7×(X+1)-(1000+0.7X)=0.7(元)。选项A正确,选项B错误。当人均可支配收入增加1%,人均消费增长=[1000+0.7×(1+1%)-(1000+0.7X)]÷(1000+0.7X)=0.7%X÷(1000+0.7)。选项C、D错误。当X=2000时,代入回归模型中,得到Y=1500,选项E正确。
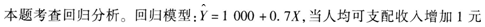
时,人均消费增加=1000+0.7×(X+1)-(1000+0.7X)=0.7(元)。选项A正确,选项B错误。当人均可支配收入增加1%,人均消费增长=[1000+0.7×(1+1%)-(1000+0.7X)]÷(1000+0.7X)=0.7%X÷(1000+0.7)。选项C、D错误。当X=2000时,代入回归模型中,得到Y=1500,选项E正确。
相关考题:
对2009年我国13个省市自治区城镇居民人均消费支出与人均可支配收入的相关系数进行显著性检验时,t的检验值为28.51,tα/2=2.201,则下列说法正确的有( )。(α=0.05)A.拒绝H0B.接受H0C.人均消费性支出与人均可支配收入之间存在显著的线性相关关系D.人均消费性支出与人均可支配收入之间不存在显著的线性相关关系E.无法判断人均消费性支出与人均可支配收入之间是否存在显著的线性相关关系
为分析某市城镇居民1995年~2003年人均可支配收入和人均消费性支出之间的关系,取得如下统计资料:请根据以上资料进行计算和分析判断,从备选答案中选出正确答案。A.B.C.当人均可支配收入增加1元时,人均消费性支出将平均增长0.7209元D.当人均可支配收人增加1元时,人均消费性支出将增长0.7209元
根据调查得到的人均居民消费额、人均国内生产总值和前一期人均消费额的有关资料,建立的二元线性回归方程为Y=0.011+0.339X1+0.302X2。请回答:可以计算的简单相关系数个数为( )。A.1B.2C.3D.4
估计的城镇居民家庭人均可支配收入和人均消费的一元线性直线回归方程式:人均消费Y=1300+0.79X,则当城镇居民家庭人均可支配收入是15000元,人均消费支出是( )元。A.13000B.13150C.12560D.15000
关于一元线性回归模型,下列表述错误的是( )。A.Y=β0+β1X+ε,只涉及一个自变量的回归模型称为一元线性回归模型B.因变量Y是自变量X的线性函数加上误差项C.β0+β1X反映了由于自变量X的变化而引起的因变量y的线性变化D.误差项是个随机变量,表示除线性关系之外的随机因素对Y的影响,能由X和Y的线性关系所解释的Y的变异性
在某城市随机抽取1000户居民作为样本对该城市居民消费水平进行研究,对居民月消费支出Y(单位:元)和月收入X(单位:元),建立回归模型,得到估计的回归方程Y=1300+0.6X,决定系数0.96,关于该模型的说法正确的有( )。A.居民月收入和月消费支出之间正相关B.回归模型的拟合效果很好C.居民月收入难以解释月消费支出的变化D.居民月收入每增长1元,月消费支出将平均增长0.6元E.居民月收入为10000时,居民人均月消费支出大约为7300元
利用样本数据拟合城镇居民人均可支配收入X(单位:元)和人均消费Y(单位:元)的回归方程,估计方程Y=1293+0.6X,R2为0.99,说法正确的有( )。A.城镇居民家庭人均可支配收入每增加1元,城镇居民人均消费增加0.6元B.城镇居民家庭人均可支配收入每增加1元,城镇居民人均消费增加1293元C.城镇居民可支配收入对人均消费支出的变化的解释能力较差D.城镇人均可支配收入可以很好地解释人均消费支岀的变化E.城镇居民家庭人均可支配收入X=20000元时,人均消费支出Y预估为13293元
根据抽样调查数据中人均收入和人均可支配消费进行回归分析,得到估计的一元线性回归模型Y=1000+0.7X,(X,人均可支配收入;Y,人均消费,单位为元),关于该回归模型的说法,正确的是()。A. 人均可支配收入每增加1元,人均消费将平均增长0.7元B. 人均可支配收入每减少1元,人均消费将平均增长0.7元C. 人均可支配收入每增加1元,人均消费将平均增长0.7% D. 当人均可支配收入为20000元时,,人均消费将为15000E. 人均可支配收入每减少1%,人均消费将平均增长7%
(一)将我国31个省(自治区、直辖市)某年度城镇居民家庭人均食品消费支出(y,单位:元)、城镇居民家庭人均可支配收入(x1,单位:元)和食品类居民消费价格指数(x2,单位:上年=100)进行回归分析,得到如表1~表3所示的输出结果:表 1 回归方程的输出结果描述城镇居民家庭人均食品消费支出与城镇居民家庭人均可支配收入之间关系适合的图形是( )。A.直方图 B.折线图C.散点图 D.雷达图
(一)将我国31个省(自治区、直辖市)某年度城镇居民家庭人均食品消费支出(y,单位:元)、城镇居民家庭人均可支配收入(x1,单位:元)和食品类居民消费价格指数(x2,单位:上年=100)进行回归分析,得到如表1~表3所示的输出结果:表 1 回归方程的输出结果根据表1~表3的输出结果可以得出( )。A.回归方程为:B.城镇居民家庭人均食品消费支出与城镇居民家庭人均可支配收入和食品类居民消费价格指数的总体相关程度为87.7%C.多元回归分析中拟合优度大小应根据判定系数( )来衡量D.多元回归分析中拟合优度大小应根据调整后的判定系数( )来衡量
(一)将我国31个省(自治区、直辖市)某年度城镇居民家庭人均食品消费支出(y,单位:元)、城镇居民家庭人均可支配收入(x1,单位:元)和食品类居民消费价格指数(x2,单位:上年=100)进行回归分析,得到如表1~表3所示的输出结果:表 1 回归方程的输出结果城镇居民家庭人均食品消费支出、城镇居民家庭人均可支配收入和食品类居民消费价格指数数据属于( )。A.一手数据 B.二手数据C.实验数据 D.定性数据
(一)将我国31个省(自治区、直辖市)某年度城镇居民家庭人均食品消费支出(y,单位:元)、城镇居民家庭人均可支配收入(x1,单位:元)和食品类居民消费价格指数(x2,单位:上年=100)进行回归分析,得到如表1~表3所示的输出结果:表 1 回归方程的输出结果如果 ,根据表2,下列说法正确的是( )。A.F检验的假设为: B.F检验的假设为: C.回归方程的线性关系显著D.回归方程的线性关系不显著
(一)将我国31个省(自治区、直辖市)某年度城镇居民家庭人均食品消费支出(y,单位:元)、城镇居民家庭人均可支配收入(x1,单位:元)和食品类居民消费价格指数(x2,单位:上年=100)进行回归分析,得到如表1~表3所示的输出结果:表 1 回归方程的输出结果如果 ,根据表3,下列说法正确的是( )。A.城镇居民家庭人均可支配收入对城镇居民家庭人均食品消费支出的线性关系 显著B.城镇居民家庭人均可支配收入对城镇居民家庭人均食品消费支出的线性关系不显著C.食品类居民消费价格指数对城镇居民家庭人均食品消费支出的线性关系显著D.食品类居民消费价格指数对城镇居民家庭人均食品消费支出的线性关系不显著
某地区人均消费支出(y,单位:千元)与人均可支配收入(x1,单位:千元)、恩格尔系数(x2,单位:%)的回归模型为: 。其中, 表示该地区人均可支配收入每增加1千元,人均消费支出平均增加0.602千元。
根据某地区2005-2015年农作物种植面积(X)与农作物产值(Y),可以建立一元线性回归模型,估计结果得到判定系数R=0.9,回归平方和ESS=90,则回归模型的残差平方和RSS为( )。 A、10B、100C、90D、81
某分析师建立了一元线性回归模型为 C i =β0 +β 1 Y i +u i ,根据已知样本,得到如下估计方程:(回答71-72题)在显著性水平α =0.05 的条件下,对于该一元回归模型的回归系数显著性分析正确的是( )。
多选题根据抽样调查数据对人均消费和人均可支配收入进行回归分析,得到估计量的一元回归线模型Y=1000+0.7X(X为人均可支配收入,y为人均消费额),关于该回归模型的说法,说法正确的是( )。A人均可支配收入每减少1元,人均消费平均增长0.7元B人均可支配收入每增加1元,人均消费平均增长0.7元C人均可支配收入每增加1%,人均消费平均增长0.7%D当人均可支配收入为20 000元时,人均消费将为15 000元E人均可支配收入每减少1%,人均消费将平均增长0.7%
单选题某团队希望了解焊接工艺中的温度(x1)、时间(x2)和焊锡量(x3)对焊接强度的影响,该过程已经积累的大量历史数据,该团队拟采用回归技术分析三个因素的影响程度,请问在进行回归分析时,以下哪种处理方法是正确的?()A针对焊接强度(y)对三个影响因素分别建立回归方程B先分析三个因素之间的相关关系,然后用最佳子集法建立y对三个因素的线性回归模型,然后根据模型诊断结果对模型进行改进C先建立y和三个因素的线性回归模型,剔除不显著的因素,即可构建所需模型D先建立y和三个因素的非线性回归模型,剔除不显著因素,即可构建所需模型
单选题对于某市城镇居民人均可支配收入和人均消费性支出之间依存关系的回归方程为:,在此估计方程中,0.7083表明()。A当居民人均可支配收入增加1元时,人均消费性支出将平均增长0.7083元B当居民人均可支配收入增加0.7083元时,人均消费性支出将平均增长1元C当居民人均可支配收入增加525.8662元时,人均消费性支出将平均增长0.7083元D当居民人均可支配收入增加0.7083元时,人均消费性支出将平均增长0.53元
多选题根据抽样调查数据对人均可支配收入和人均消费进行回归分析,得到估计的一元线性回归模型Y(∧)=1000+0.7X(X:人均可支配收入,Y(∧):人均消费,单位均为元),关于该回归模型的说法,正确的是( )。[2015年真题]A人均可支配收入每增加1元,人均消费将平均增长0.7元B人均可支配收入每减少1元,人均消费将平均增长0.7元C人均可支配收入每增加1%,人均消费将平均增长0.7%D当人均可支配收入为20000元时,人均消费将为15000元E人均可支配收入每减少1%,人均消费将平均增长0.7%
多选题在某城市随机抽取1000户居民作为样本对该城市居民消费水平进行研究,对居民月消费支出Y(单位:元)和月收入X(单位:元),建立回归模型,得到估计的回归系数Y=1300+0.6X,决定系数0.96,关于该模型的说法正确的有( )A居民月收入和月消费支出之间正相关B回归模型的拟合效果很好C居民月收入难以解释月消费支出的变化D居民月收入每增长1元,月消费支出将平均增长0.6元E居民月收入为10000元时,居民人均月消费支出大约为7300元
单选题回归分析模型可以是()A一元线性回归模型B多元线性回归模型C系统聚类分析D一元回归模型,多元回归模型