设函数的两根分别在区间(1，2)和(2，3)内，则()
设函数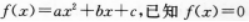
的两根分别在区间(1，2)和(2，3)内，则()
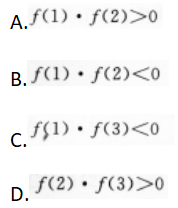
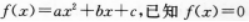的两根分别在区间(1，2)和(2，3)内，则()
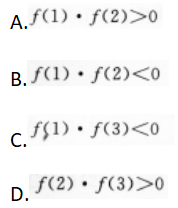
参考解析
解析：【考情点拨】本题主要考查的知识点为二次函数的性质． 【应试指导】∵方程的两根分别在区间(1，2)和 (2，3)内，如图，
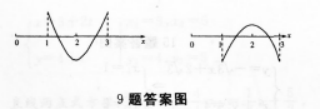
相关考题：
设R(t)表示可靠度函数，F(t)表示累积故障分布函数，则下列表述正确的有( )。A．R(t)是[0，∞)区间内的非减函数，且0≤R(t)≤1B．R(t)是[0，∞)区间内的非增函数，且0≤R(t)≤1C．在[0，∞)区间内，R(t)+F(t)=1D．F(t)在[0，∞)区间内的非减函数，且0≤F(t)≤1E．F(t)在[0，∞)区间内是非增函数
为了用二分法求函数f(x)＝x3-2x2-0.1的根(方程f(x)＝0的解)，可以选择初始区间(64)。也就是说，通过对该区间逐次分半可以逐步求出该函数的一个根的近似值。A．[-2，-1]B．[-1，1]C．[1，2]D．[2，3]
设A，B是两个集合，A={1，2，3}，B={1，2}，则ρ(A) -ρ(B) =(60)。A．{{3}，{1，3}，{2，3}，{1，2，3}}B．{{1，3}，{2，3}，{1，2，3}}C．{{1，2}，{2，3}，{1，2，3}}D．{{1}，{1，3}，{2，3}，{1，2，3}}。
单选题设数据元素的集合D={1,2,3,4,5}，则满足下列关系R的数据结构中为线性结构的是（ ）。AR={(1,2),(3,4),(5,1),(1,2)}BR={(1,3),(4,1),(3,2),(5,4)}CR={(1,2),(2,3),(4,5),(2,3)}DR={(1,3),(2,4),(3,5),(1,2)}