已知等比数列()A.4B.-4C.4或-4D.2

已知等比数列()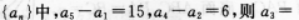

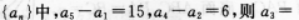A.4
B.-4
C.4或-4
D.2

参考解析

解析：【考情点拨】本题主要考查的知识点为等比数列． 【应试指导】由已知条件得


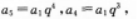
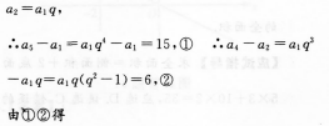
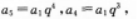
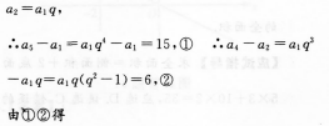
相关考题：

已知公比为q的等比数列{an）中，a2=4，a5=-32．（I）求q；（11）求{an}的前6项和S6．
查看答案
等比数列的极限一定存在。() 此题为判断题(对，错)。
查看答案
指数平滑法的特点之一是它对预测目标的全部历史观察值由近及远分别给以权数,这种权数是()。 A.等差数列B.依次递增的等比数列C.依次递减的等比数列
查看答案
在等比数列中，已知首项为9/3，末项为1/3，则项数为 。A. 3B. 4C. 5D. 6
查看答案
已知等比数列{an}的各项都是正数，且a1+a3=10，a2+a3=6．(I)求{an}的通项公式；(II)求{an)的前5项和．
查看答案
已知等比数列a1=1，a9=25，则a5=（）A.25B.-5C.±5D.5
查看答案
A.等差数列B.等比数列C.既是等差数列又是等比数列D.既非等差数列亦非等比数列E.以上选项均不正确
查看答案
已知首项为1的无穷递缩等比数列的所有项之和为5,q为公比,则q=（ ）A.2/3B.-2/3C.4/5D.-4/5E.1/2
查看答案
高中数学《等比数列》一、考题回顾二、考题解析【教学过程】(一)引入新课利用多媒体放映具体实例：(1)细胞分裂模型。提问：通过观察影片中的实例，你能用数字表达出上述实例的含义吗?学生活动：学生通过观察计算，得出1，2，4，8，……提问：这个数列是我们之前学过的等差数列吗?它又有什么特点呢?引出《等比数列》。(二)探索新知1.等比数列的概念大屏幕展示实例：(2)《庄子》中“一尺之棰”的论述。1.既是等差数列又是等比数列的数列存在吗?如果存在，你能举出例子吗?2.等比数列的性质有哪些?(至少说出3点)
查看答案
高中数学《等比数列前n项和》一、考题回顾二、考题解析【教学过程】(一)引入新课提出问题：如何将之前学过的等比数列求和方法推广到一般等比数列求和?引出课题。(二)探索新知学生活动：自主探究、推导。师生共同分析、得出推导过程：1.本节课的难点是什么?如何突破难点?2.总结一下，数列求和的方法有哪些?
查看答案
高中数学《等比数列》一、考题回顾
查看答案
已知数列{％}的前n项和是 (1)求证：数列{an}是等比数列： (2)记的前n项和Tn的最大值及相应的n值。
查看答案
A.等比数列、斐波那契数列B.黄金分割、斐波那契数列C.等比数列、黄金分割D.调和数列、黄金分割
查看答案
在Excel中利用填充柄可以实现等比数列的自动填充。()
查看答案
根据规律，等比数列3、9、27、（），括号中应该填（）。
查看答案
小赵、小钱、小孙、小李、小周五个人的收入依次成等比数列，已知小赵的收入是3000元，小孙的收入是3600元，那么小周比小孙的收入高：（）A、700元B、720元C、760元D、780元
查看答案
等差数列、等比数列是已经标准化了的一般数值系列。
查看答案
古埃及人在计算等比数列求和时已经大量使用了现代等比数列求和公式。
查看答案
numpy中创建等比数列的函数是（）A、linspaceB、logspaceC、sequenceD、无创建等比数列函数
查看答案
填空题某等比数列，已知n1=11.8，nmax=530，变速级数Z=12，则该数列的公比φ应为（）。
查看答案
单选题小赵、小钱、小孙、小李、小周五个人的收入依次成等比数列，已知小赵的收入是3000元，小孙的收入是3600元，那么小周比小孙的收入高：（）A700元B720元C760元D780元
查看答案
单选题numpy中创建等比数列的函数是（）AlinspaceBlogspaceCsequenceD无创建等比数列函数
查看答案
问答题机床主轴转速采用等比数列的主要原因是什么？
查看答案
填空题根据规律，等比数列3、9、27、（），括号中应该填（）。
查看答案
填空题机床主轴转速等比数列，其公比范围是（）。
查看答案
判断题古埃及人在计算等比数列求和时已经大量使用了现代等比数列求和公式。A对B错
查看答案
单选题“斐波那契数列”可以拆分成：（）。A两个等比数列B两个等差数列C一个等差数列和一个等比数列D无法拆分
查看答案
热门标签