刚架桥与连续梁桥的区别是( )。A.桥跨刚度大B.桥墩刚度大C.梁、柱结点为刚接D.梁、柱结点为铰接
图示桁架,在结点C处沿水平方向受P力作用。各杆的抗拉刚度相等。若结点C的沿垂位移以VC表示,BC杆的轴力以NBC表示,则:
图所示的刚架,EI=常数,各杆长为l,A截面的转角为( )。
图所示的结构AB,杆件A截面的转角θA值为( )。
已知刚架的弯矩图如图所示,杆的抗弯刚度为杆的为2EI,则结点B的角位移等于:
图示刚架,各杆线刚度相同,则结点A的转角大小为( )。
图所示刚架,EI=常数,结点A的转角是( )。(提示:利用转动刚度的概念)
设各杆的EA值相同,在图所示的桁架中,节点C的竖向位移为( )。
图示刚架,EI为常数,结点A的转角是( )。(提示:利用对称性和转动刚度的概念)
图示刚架,EI=常数,结点A的转角是( )。(提示:利用转动刚度的概念)
图所示刚架,EI为常数,结点A的转角是( )。(提示:利用对称性和转动刚度的概念)
如图所示的一三铰刚架,其右支座发生了位移,位移的水平分量为Δ1,竖向分量为Δ2,则右半部的转角为( )。
如图所示的刚架,各杆EI相同,C点竖向位移(向下为正)等于( )。
图示为刚架在均布荷载作用下的M图,曲线为二次抛物线,横梁的抗弯刚度为2EI,竖柱为EI,支座A处截面转角为:
图所示结构,各杆,当支座B发生图示的移动时,结点E的水平位移为( )。
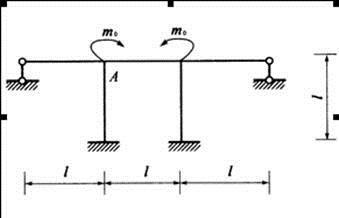
左图所示对称刚架受同向结点力偶作用,弯矩图的正确形状是右侧四个图中的:
图式刚架,各杆线刚度i相同,则结点A的转角大小为:
图示各杆件的E、I、l均相同,在图b)的四个图中,与图a)杆件左端的转动刚度(劲度)系数相同的是:
图示结构各杆线刚度i相同,力矩分配系数μAB等于:
图示为结构在荷载作用下的M图,各杆EI=常数,则支座B处截面的转角为:
杆AB长为l,质量为m,图4-64所示瞬时点A处的速度为V,则杆动量的大小为( )。
用位移法求解刚架,并绘弯矩图。各杆EI相同等于常数。
汇交于某结点各杆端的力矩分配系数之比等于各杆端转动刚度之比。
关于刚架杆件转动刚度,下列说法中不正确的是()。A、数值上等于使杆端产生单位转角时需要施加的力矩B、其值仅与杆件的线刚度有关C、远端支承为铰支时其值为3iD、转动刚度表示杆端抵抗转动的能力
单选题如图所示桁架,在结点C沿水平方向受P力作用。各杆的抗拉刚度相等。若结点C的铅垂位移以VC表示,BC杆的轴力以NBC表示,则()。A NBC=0,Vc=0B NBC=0,VC≠OC NBC≠O,VC=OD NBc≠0,VC≠0
判断题增加各杆刚度,则结构的结点位移就一定减少。A对B错