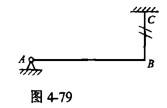
如图4-79所示水平杆AB=l,质量为2m,剪断绳BC瞬间，A处约束力为（ ）。A. 2mg B. mg C. 1/2mg D. 1/4mg

如图4-79所示水平杆AB=l,质量为2m,剪断绳BC瞬间，A处约束力为（ ）。

A. 2mg B. mg C. 1/2mg D. 1/4mg

参考解析

解析：提示：可用动静法，将惯性力向A点简化。

相关考题：

图示一起重机,A、B、C处均为光滑铰链,水平梁AB的重量P=4kN,荷载F=10kN,有关尺寸如图所示,BC杆自重不计。试求杆BC所受的拉力和铰链A给杆AB的约束力。
查看答案
阶梯杆受力如图所示，设AB和BC段的横截面面积分别为2A和A，弹性模量为E，则杆中最大正应力为()，截面C的位移为()。
查看答案
阶梯杆受力如图所示，设AB和BC段的横截面面积分别为2A和A，弹性模量为E，则杆中最大正应力为( )。
查看答案
质量为m，长为2l的均质杆初始位于水平位置， 如图所示。A端脱落后，杆绕轴B转动，当杆转到铅垂位置时，AB 杆B处的约束力大小为：
查看答案
均质细直杆AB长为l，质量为m，以匀角速度ω绕O轴转动，如图所示，则AB杆的动能为：
查看答案
质量为m，长为2l的均质细杆初始位于水平位置，如图所示。A端脱落后，杆绕轴B转动，当杆转到铅垂位置时，AB杆角加速度的大小为：
查看答案
杆AB的A端置于光滑水平面上，AB与水平面夹角为 30°，杆重为P，如图所示，B处有摩擦，则杆AB平衡时，B处的摩擦力与x方向的夹角为（　　）。A、90°B、30°C、60°D、45°
查看答案
机构如图，杆ED的点H由水平绳拉住，其上的销钉C置于杆AB的光滑直槽中，各杆重均不计。已知Fp=10KN。销钉C处约束力的作用线与轴正向所成的夹角为（　　）。A、0B、90°C、60°D、150°
查看答案
T形均质杆OABC以匀角速度ω绕O轴转动，如图所示。已知OA杆的质量为2m，长为2l，BC杆质量为m，长为l，则T形杆在该位置对O轴的动量矩为：
查看答案
均质细杆AB重力为P、长2L，A端铰支，B端用绳系住，处于水平位置，如图所示，当B端绳突然剪断瞬时，AB杆的角加速度大小为：
查看答案
如图所示，结构由AB、BC、CE三杆铰接而成，A处为固定端，杆重不计，铰C上作用一铅垂力P，则二力杆为（　　）。A．AB、BC、CEB．BC、CEC．ABD．均不是二力杆
查看答案
如图所示变截面杆中，AB段、BC段的轴力为：
查看答案
均质细杆重力为P、长2L，A端铰支，B端用绳系住，处于水平位置，如图所示。当B端绳突然剪断瞬时，AB杆的角加速度大小为：
查看答案
均质杆AB长为l，重为W，受到如图所示的约束，绳索ED处于铅垂位置，A、B两处为光滑接触，杆的倾角为α，又CD = l/4，则 A、B两处对杆作用的约束力大小关系为：A. FNA=FNB= 0 B. FNA=FNB≠0 C. FNA≤FNB D.FNA≥FNB
查看答案
均质细杆AB重力为P，长为2l，A端铰支，B端用绳系住，处于水平位置，如图所示。当B端绳突然剪断瞬时，AB杆的角加速度大小为3g/4l，则A处约束力大小为：A. FAx= 0,FAy=0 B. FAx= 0,FAy=P/4 C. FAx= P,FAy=P/2 D.FAx= 0,FAy=P
查看答案
T形均质杆OABC以匀角速度ω绕O轴转动，如图所示。已知OA杆的质量为2m，长为2l，BC杆质量为m，长为l，则T形杆在图示位置时动量的大小为：
查看答案
匀质杆OA质量为M，长为l，角速度为ω，如图所示。则其动量大小为：
查看答案
如图4-61所示匀质杆AB长l，质量为C。点D距点A为1/4l。杆对通过点D且垂直于的轴y的转动惯量为（ ）。
查看答案
质量为m，长为2l的均质细杆初始位于水平位置，如图4-68所示。A端脱落后， 杆绕轴B转动，当杆转到铅垂位置时，AB杆B处的约束力大小为（ ）。
查看答案
均质细杆AB重力为P、长2L, A端铰支，B端用绳系住，处于水平位置，如图4-73所示。当B端绳突然剪断瞬时AB杆的角加速度大小为()。A.0 B.3g/4L C.3g/2L D.6g/L
查看答案
均质细直杆AB长为l，质量为m,以匀角速度ω绕O轴转动，如图4-69所示， 则AB杆的动能为（ ）。
查看答案
杆AB长为l,质量为m，图4-64所示瞬时点A处的速度为V,则杆动量的大小为（ ）。
查看答案
均质细杆AB重力为W，A端置于光滑水平面上，B端用绳悬挂如图4-56所示。当绳断后杆在倒地的过程中，质心C的运动轨迹为（）。A、圆弧线B、曲线C、铅垂直线D、抛物线
查看答案
单选题如图5-16所示，轴向拉压杆横截面积为A，则该杆中最大正应力σ max的值为（）。A AB BC CD D
查看答案
单选题如图所示，力P作用在BC杆的中点，且垂直于BC杆，若P=kN，杆重不计。则杆AB的内力大小S为（　）A 1kNB 0．5kNC 1．41kND 2kN
查看答案
热门标签