如图5-27所示两根梁，它们的答案为（ ）。A. FS、M图都相同 B. FS、M图都不相同C. FS图相同，M图不同 D. M图相同， FS图不同

如图5-27所示两根梁，它们的答案为（ ）。

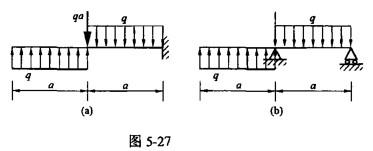
A. FS、M图都相同 B. FS、M图都不相同
C. FS图相同，M图不同 D. M图相同， FS图不同

参考解析

解析：提示：计算图(a)和图(b)中两梁约束反力可知两梁受力完全相同，所以得答案。

相关考题：

有如图所示简支梁，其抗弯刚度EI为常数。该梁的挠曲线方程为()。A.B.C.D.
查看答案
如图所示一等截面简支梁，则梁中点C处的挠度为( )。
查看答案
承受均布载荷的简支梁如图a)所示，现将两端的支座同时向梁中间移动l/8，如图b)所示，两根梁的中点l/2处)弯矩之比Ma/Mb为：A. 16B. 4C. 2D. 1
查看答案
简支梁受分布荷载作用如图所示。支座A、B的约束力为：
查看答案
材料相同的两根杆件受力如图所示。若杆①的伸长量为，杆②的伸长量为，则下列结论中正确的是：
查看答案
如图所示梁，剪力等于零的截面位置x之值为:
查看答案
用卡式定理计算如图所示梁C截面的挠度为( )。
查看答案
如图所示两根梁中的l,b和P均相同，若梁的横截面高度h减小为h/2，则梁中的最大正应力是原梁的多少倍？A. 2B.4C. 6D. 8
查看答案
已知简支梁受如图所示荷载，则跨中点C截面上的弯矩为：
查看答案
材料和尺寸完全相同的两根矩形截面梁叠在一起承受荷载，如图a)所示。设材料的许用应力为[σ]，其容许荷载为[P1]。如将两根梁用一根螺栓连接成一个整体，如图b)所示。设螺栓的强度足够，其容许荷载为[P2]。则[P1]、[P2]都正确的答案为：
查看答案
如图所示，用力法且采用图（b）所示的基本体系计算图（a）所示梁，Δ1P为（　　）。
查看答案
如图所示，等截面梁的1/3跨度处挠度为（　　）。
查看答案
如图所示，梁A端弯矩为（　　）。 A、M B、0 C、2M D、3M
查看答案
四根简支梁配筋及破坏时受压区高度如图所示，它们的承载力Mu的大小顺序为（　　）。
查看答案
如图所示梁中点的挠度为（　　）。
查看答案
如图5-28所示两根梁的最大弯矩之比Mmax a/Mmax b等于（ ）。 A. 1 B. 2 C. 3 D. 4
查看答案
外伸梁受载荷如图5-46 (a)所示，其挠曲线的大致形状有图5-46 (b)所示A、 B、C、D四种，正确答案为（ ）。
查看答案
就正应力强度而言,如图5-31所示的梁，以下哪个图所示的加载方式最好的为（ ）。
查看答案
如图5-43所示，两根材料相同、弯曲刚度相同的悬臂梁I、II如图示，正确结论为（ ）。A. I梁和II梁的最大挠度相同 B. II梁的最大挠度是I梁的2倍C. Ⅱ梁的最大挠度是I梁的4倍 D. Ⅱ梁的最大挠度是I梁的1/2倍
查看答案
热门标签