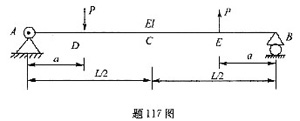
如图所示一等截面简支梁，则梁中点C处的挠度为( )。

如图所示一等截面简支梁，则梁中点C处的挠度为( )。



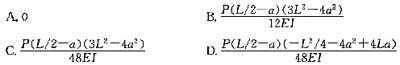
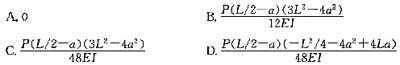
参考解析

解析：此梁的受力情况对于跨中点C为反对称，故截面C处的挠度为零

相关考题：

简支梁绝对值最大弯矩的意义是() A、中某截面的最大弯矩值B、梁中点较近的某截面的弯矩值C、中各截面的最大弯矩中的最大值D、中点截面的最大弯矩值
查看答案
简支梁桥抗弯能力不足或主梁挠度过大时,宜优先采用下列哪些方法进行加固()。 A、施加体外预应力B、增大截面C、更换主梁D、简支变连续
查看答案
一般情况下,简支梁的最大挠度发生在梁跨中截面处。() 此题为判断题(对，错)。
查看答案
跨度为l的简支梁已知EI，当整个梁承受均布荷载q时，梁中点挠度Wc=-5ql^4/384EI，图示简支梁跨中挠度Wc=()。
查看答案
用卡式定理计算如图所示梁C截面的挠度为( )。
查看答案
矩形截面简支梁，梁中点承受集中力F。若h＝2b。分别采用图（a）、图（b）两种方式放置，图（a）梁的最大挠度是图（b）梁的（　　）。A、0.5倍B、2倍C、4倍D、8倍
查看答案
矩形截面简支梁中点承受集中力F。若h= 2b，分别采用图a)、图b)两种方式放置，图a)梁的最大挠度是图b)梁的：A. 1/2B. 2 倍C. 4 倍D. 8 倍
查看答案
已知简支梁受如图所示荷载，则跨中点C截面上的弯矩为：
查看答案
简支梁受荷载如图所示，在支座A处的约束反力为（　　）。
查看答案
如图所示，等截面梁的1/3跨度处挠度为（　　）。
查看答案
进行简支梁挠度计算时，用梁的最小刚度Bmin代替材料力学公式中的EI。 Bmin值的含义是：A.沿梁长的平均刚度B.沿梁长挠度最大处截面的刚度C.沿梁长内最大弯矩处截面的刚度D.梁跨度中央处截面的刚度
查看答案
如图所示梁中点的挠度为（　　）。
查看答案
如图5-41所示两简支梁的材料、截面形状及梁中点承受的集中载荷均相同，而两梁的长度l1/l2=1/2,则其最大挠度之比为（ ）。
查看答案
矩形截面简支梁梁中点受集中力F，如图5-38所示。若h=2b,分别采用图(a)、 图(b)两种方式放置，图(a)梁的最大挠度是图(b)梁的（ ）。A. 0.5 倍 B. 2 倍 C. 4 倍 D. 8 倍
查看答案
圆截面简支梁如图所示，已知F=1KN，回答下列问题。 若梁直径d=40mm，求梁的最大应力。
查看答案
进行简支梁的挠度计算时，按照最小刚度原则（）。A、沿梁长的平均刚度B、沿梁长挠度最小处的刚度C、取梁长内同号弯矩最大处的截面刚度D、沿梁长挠度最大处的刚度
查看答案
一简支梁分在中点处作用一力偶，则其中点的挠度值为（）。
查看答案
两米长的等截面简支梁在距左支座0.5米处作用集中载荷，则危险截面为左处。
查看答案
简支梁截面C处作用有一个集中力偶，则截面C稍左和稍右梁截面的剪力（），弯矩（）。A、相同；相同B、相同；不同C、不同；相同D、不同；不同
查看答案
进行钢筋混凝土简支梁挠度验算时，应取（）截面的刚度。A、支座截面B、跨中截面C、1/4跨截面D、最小刚度截面
查看答案
进行简支梁挠度计算时，用梁的最小刚度Bmin代替材料力学公式中的EI。Bmin值的含义是：（）A、沿梁长的平均刚度B、沿梁长挠度最大处截面的刚度C、沿梁长内最大弯矩处截面的刚度D、梁跨度中央处截面的刚度
查看答案
简支梁水平放置，中点受竖向力P作用，梁长度为L，最大弯矩发生在（）A、中点截面Mmax=PL/2B、中点截面Mmax=PL/4C、L/4截面Mmax=PL/8D、L/4截面Mmax=PL/2
查看答案
简支梁受力点使主应力最大的截面位置是（）。A、梁的左端部B、梁的1/4处C、梁的中点D、梁的右端部
查看答案
两矩形截面简支梁，截面面积相同，截面高度之比为2。若两梁材料相同，梁长相同，在梁中截面受相同集中力作用，则其最大挠度之比为1/4。
查看答案
简支梁全梁受均布力的作用，最大挠度发生在（）。A、两端B、中点C、左端D、右端
查看答案
单选题进行简支梁的挠度计算时，按照最小刚度原则是：（）。A沿梁长的平均刚度B沿梁长挠度最小处的刚度C取梁长内同号弯矩最大处的截面刚度
查看答案
单选题一简支梁全长L，在离左支点L／4处向下垂直施力，则梁上截面弯矩最大的地方应是（）。A左支点B施力的地方C梁中点D右支点
查看答案
热门标签