下列微分方程中,可分离的变量方程是《》( )
下列微分方程中,可分离的变量方程是《》( )
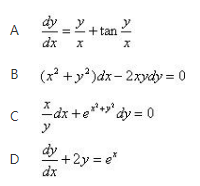
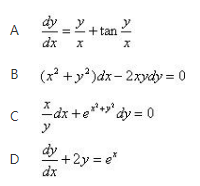
参考解析
解析:
相关考题:
关于利用积分变换分析电路,下列说法正确的是()。 A、把时域微分方程转换为频域代数方程;再作反变换,可求得满足电路初始条件的原微分方程的解答,不需要确定积分常数。B、把时域微分方程转换为频域低阶微分方程;再作反变换,可求得满足电路初始条件的原微分方程的解答。C、把时域微分方程转换为频域代数方程;再作反变换,可求得满足电路初始条件的原微分方程的解答,需要确定积分常数。D、把时域微分方程转换为频域代数方程,求解频域代数方程即可求得满足电路初始条件的原微分方程的解答。
线性系统环节的微分方程的建立步骤包括: ( 1 )确定输入、输出变量; ( 2 )根据遵循的物理或化学定律,定义(),列写(); ( 3 )消去(),得到输入与输出变量之间的微分方程; ( 4 )整理成()的微分方程。
单选题理论求解对流换热问题时,需要的方程组组成应为( )。A连续性方程、动量微分方程和能量微分方程B对流换热过程微分方程、连续性方程、动量微分方程和能量微分方程C傅里叶定律、连续性方程、动量微分方程和能量微分方程D对流换热过程微分方程、傅里叶定律、动量微分方程和能量微分方程
单选题若一阶方程y'=f(x,y)中,f(x,y)=u(x)v(y),则它是()。A线性方程B齐次方程C变量可分离方程D恰当方程