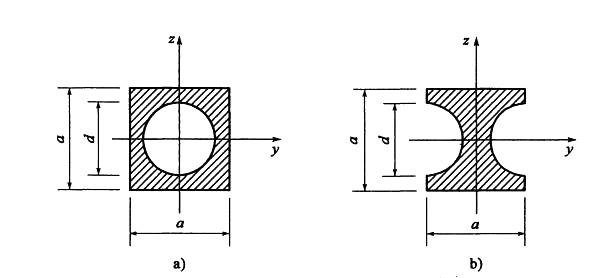
面积相等的两个图形分别如图a)和图b)所示。它们对对称轴轴的惯性矩之间的关系为：

面积相等的两个图形分别如图a)和图b)所示。它们对对称轴轴的惯性矩之间的关系为：


参考解析

解析：

相关考题：

平面图形对任何一轴的惯性矩,等于它对平行于该轴的形心轴的惯性矩加上平面图形面积与两轴之间距离平方的乘积。() 此题为判断题(对，错)。
查看答案
如图所示正方形截面对y1轴的惯性矩应为：
查看答案
如图所示正方形截面对z1轴的惯性矩与对z轴惯性矩的关系是：
查看答案
如图所示，截面面积为A，形心为C，对z轴的惯性矩为Iz，则截面对z1轴的惯性矩IZ1为（　　）。
查看答案
下列关于平面图形几何性质的说法中，错误的是（　　）。A．对称轴必定通过图形形心B．两个对称轴的交点必为图形形心C．图形关于对称轴的静矩为零D．使静矩为零的轴必为对称轴
查看答案
如图所示一矩形截面，面积为A，高度为b，对称轴为z，z1和z2均平行于z，下列计算式中正确的为：
查看答案
关于截面的几何性质，下列说法正确的是( )。A.图形对其对称轴的静矩为零，惯性矩不为零，惯性积为零B.图形对其对称轴的静矩不为零，惯性矩和惯性积均为零C.图形对其对称轴的静矩、惯性矩及惯性积均为零D.图形对其对称轴的静矩、惯性矩及惯性积均不为零
查看答案
图示的矩形截面和正方形截面具有相同的面积。设它们对对称轴y的惯性矩分别为
查看答案
面积相等的两个图形分别如图a)和图b)所示。它们对对称轴轴的惯性矩之间的关系为：
查看答案
在yOz正交坐标系中，设图形对：y、z轴的惯性矩分别为Iy和Iz，则图形对坐标原点的极惯性矩为：
查看答案
面积相等的两个图形分别如图a)和图b)所示。它们对对称轴y、z轴的惯性矩之间关系为：
查看答案
在yoz正交坐标系中，设图形对y,z轴的惯性矩分别为Iy和Iz，则图形对坐标原点极惯性矩为：
查看答案
面积相等的两个图形分别如图（a）、图（b）所示，它们对对称轴y、z 轴的惯性矩之间的关系为：
查看答案
已知平面图形的形心为C，面积为A，对Z轴的惯性矩为IZ，则图形对Z1轴的惯性矩为( )。
查看答案
如图所示正方形截面对z1轴的惯性矩与对z轴的惯性矩的关系为( )。
查看答案
面积相同的三个图形如图示，对各自水平形心轴z的惯性矩之间的关系为（　　）。A、 Iza＞Izb＞IzcB、 Iza=Izb=IzcC、 Iza＜Izb＜IzcD、 Iza=Izb>Izc
查看答案
如图所示，四种单筋截面适筋梁，承受相同的弯矩，它们之间的b、h、bf′和bf也相等，则各个截面所需钢筋截面面积应满足条件（　　）。
查看答案
请列举5个以上常见的轴对称图形，它们的对称轴分别有多少条?【数学专业问题】
查看答案
如图5-17所示，已知平面图形的形心为C,面积为A,对z轴的惯性矩为Iz,对图形z1轴的惯性矩有四种答案为（ ）。A. Iz + b2A B. Iz +(a + b)2 AC. Iz + (a2 -b2)A D. Iz+(b2 -a2)A
查看答案
给定图5-21所示正方形，则图形对形心轴y和y1的惯性矩Iy1与Iy之间的关系为 ( )。A. Iy1>Iy B. Iy1 = Iy C. Iy1=0.5Iy D. Iy1y
查看答案
在正交坐标系中，设平面图形对y轴和z轴的惯性矩分别为Iy和Iz，则图形对坐标原点的极惯性矩为Ip=Iy2+Iz2。
查看答案
若平面图形具有三条或更多条的对称轴，则过平面图形形心的任一轴都是形心主惯性轴，且对任一形心主惯性轴的主惯性矩均相等。
查看答案
若截面图形有对称轴，则该图形对其对称铀的（）A、静矩为零，惯性矩不为零B、静矩不为零，惯性矩为零C、静矩和惯性矩均为零D、静矩和惯性矩均不为零
查看答案
在下列关于平面图形的结论中，（）是错误的。A、图形的对称轴必定通过形心B、图形两个对称轴的交点必为形心C、图形对对称轴的静矩为零D、使静矩为零的轴必为对称轴
查看答案
下列关于面积矩说法正确的是（）A、某图形对某轴的面枳矩若等于零，则该轴必通过图形的形心B、图形对于通过形心的轴的面积矩恒等于零C、形心在对称轴上，凡是平面图形具有两根或两根以上对称轴则形心必在对称轴的交点上D、某图形对某轴的面积矩若等于零，则该轴垂直于该图形E、图形对于通过形心的轴的面积矩不一定为零
查看答案
多选题下列关于面积矩说法正确的是（）A某图形对某轴的面枳矩若等于零，则该轴必通过图形的形心B图形对于通过形心的轴的面积矩恒等于零C形心在对称轴上，凡是平面图形具有两根或两根以上对称轴则形心必在对称轴的交点上D某图形对某轴的面积矩若等于零，则该轴垂直于该图形E图形对于通过形心的轴的面积矩不一定为零
查看答案
热门标签