承受均布载荷的简支梁如图a)所示，现将两端的支座同时向梁中间移动l/8，如图b)所示，两根梁的中点处(l/2)弯矩之比Ma/Mb为：A. 16B.4C. 2D. 1

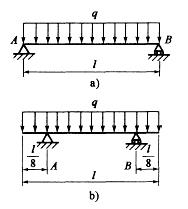
承受均布载荷的简支梁如图a)所示，现将两端的支座同时向梁中间移动l/8，如图b)所示，两根梁的中点处(l/2)弯矩之比Ma/Mb为：

A. 16
B.4
C. 2
D. 1

参考解析

解析：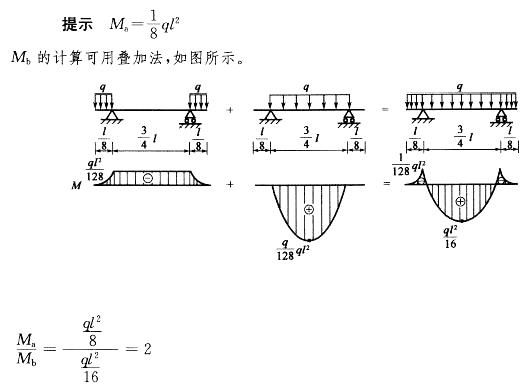

相关考题：

下列关于承受均布荷载的简支梁，说法正确的有（ ）。A．一端是固定端支座，另一端是铰支座B．梁的两端都是铰支座C．梁跨中截面处的剪力不为零D．该梁内力除剪力外，还有弯矩和轴力E．两端支座处剪力的绝对值相等
查看答案
有关简支梁的受力特性，下列说法中正确的有( )。A．梁上、下边缘压拉应力大小与截面处弯矩Mc成正比B．截面弯矩Mc越大，梁上下边缘压、拉应力也越大C．均布荷载作用下的简支梁，跨中处弯矩最大D．均布荷载作用下的简支梁，支座处剪力最大E．均布荷载作用下的简支梁，跨中处弯矩和剪力最大
查看答案
合理安排梁的支座在均布载荷作用下的简支梁,若将支座各自向里移动0.21,梁上的最大弯矩只是原来的1／6。() 此题为判断题(对，错)。
查看答案
简支梁受均布荷载作用如图所示，求梁的剪力方程和弯矩方程，画Q、M图，确定最大剪力和弯矩。
查看答案
简支梁受集中力作用如图所示，求梁的剪力方程和弯矩方程，画出Q、M图并确定最大剪力和最大弯矩。
查看答案
一矩形截面简支梁，梁上荷载如图所示。已知P=6kN、l=4m、b=0.1m、h=0.2m，画出梁的剪力图和弯矩图并求梁中的最大正应力。
查看答案
跨度为l的简支梁已知EI，当整个梁承受均布荷载q时，梁中点挠度Wc=-5ql^4/384EI，图示简支梁跨中挠度Wc=()。
查看答案
如图所示两根梁中的l,b和P均相同，若梁的横截面高度h减小为h/2，则梁中的最大正应力是原梁的多少倍？A. 2 B.4 C. 6 D. 8
查看答案
如图所示两根梁中的l,b和P均相同，若梁的横截面高度h减小为h/2，则梁中的最大正应力是原梁的多少倍？A. 2B.4C. 6D. 8
查看答案
梁ABC的弯矩如图所示，根据梁的弯矩图，可以断定该梁B点处：A.无外载荷B.只有集中力偶C.只有集中力D.有集中力和集中力偶
查看答案
如图所示，两跨连续梁的中间支座B及右端支座C分别产生竖向沉陷2Δ及Δ，由此引起的截面A的弯矩MAB之值为（　　）。
查看答案
如图所示的简支梁，当单位荷载F＝1在其AC段上移动时，弯矩Mc的影响线方程为（　　）。 A、－（l－x）a/l B、－x·b/l C、（l－x）a/l D、x·b/l
查看答案
均布荷载作用下的五跨等跨连续梁，有()等受力特征。A.第三跨跨中剪力为零B.各跨跨中弯矩都为正弯矩C.边跨跨中剪力最大D.梁端支座处梁承受负弯矩E.中间支座处梁承受负弯矩
查看答案
带有中间铰的静定梁受载情况如图所示，则：A. a越大，则MA越大B. l越大，则MA越大C. a越大，则RA越大D. l越大，则MA越大
查看答案
简支梁受荷载如图所示，在支座A处的约束反力为（　　）。
查看答案
简支梁受分布荷载作用如图所示。支座A、B的约束力为：
查看答案
如图所示一等截面简支梁，则梁中点C处的挠度为( )。
查看答案
有一简支梁，受力如图所示，支座A的反力RA是()kN。A、1/4B、1/2C、3/4D、1
查看答案
已知简支梁受如图所示荷载，则跨中点C截面上的弯矩为：
查看答案
如图5-28所示两根梁的最大弯矩之比Mmax a/Mmax b等于（ ）。 A. 1 B. 2 C. 3 D. 4
查看答案
简支梁受分布荷载作用如图4-13所示。支座A、B的约束力为（ ）。
查看答案
如图5-41所示两简支梁的材料、截面形状及梁中点承受的集中载荷均相同，而两梁的长度l1/l2=1/2,则其最大挠度之比为（ ）。
查看答案
矩形截面简支梁梁中点受集中力F，如图5-38所示。若h=2b,分别采用图(a)、 图(b)两种方式放置，图(a)梁的最大挠度是图(b)梁的（ ）。A. 0.5 倍 B. 2 倍 C. 4 倍 D. 8 倍
查看答案
均布载荷作用下的简支梁，在梁长l变为原来的2/l时，其最大挠度将变为原来（）。
查看答案
合理安排梁的支座在均布载荷作用下的简支梁，，若将支座各自向里移动0.21，梁上的最大弯矩只是原来的1/6。
查看答案
若在布满均布荷载的简支梁的跨中增加一个支座，则最大弯矩|Mmax|为原简支梁的（）。A、2倍B、4倍C、2/1倍D、4/1倍
查看答案
判断题合理安排梁的支座在均布载荷作用下的简支梁，，若将支座各自向里移动0.21，梁上的最大弯矩只是原来的1/6。A对B错
查看答案
热门标签