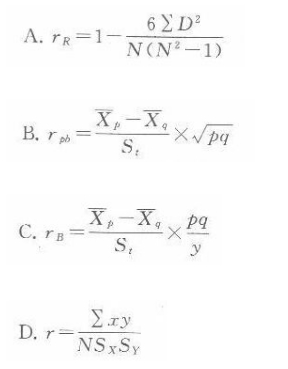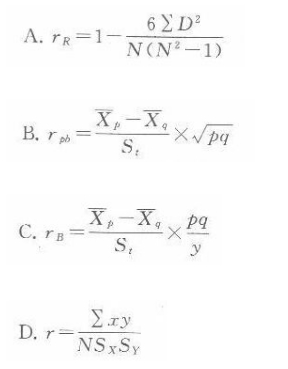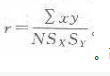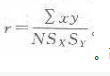对于由两只股票构成的投资组合,投资者最希望它们之间的相关系数等于( )。A.0B.-1C.+1D.无所谓
两列变量是连续变量,但样本容量较少,非正态分布,描述这两列变量之间的相关宜用()。 A.等级相关B.积差相关C.点二列相关D.系数
两个具有相关关系的变量,若它们的相关系数r>0,则说明它们是正相关的。()
A、B两变量线性相关,变量A为符合正态分布的等距变量,变量B也符合正态分布且被人为划分为两个类别,计算它们的相关系数应采用( )。 A.积差相关系数B.点双列相关C.双列相关D.肯德尔和谐系数
对于两列连续变量,可用来计算其相关系数的是()A.点二列相关、等级相关B.积差相关、斯皮尔曼等级相关C.积差相关、点二列相关D.肯德尔和谐系数、点二列相关
假设两变量为线性关系,这两变量为等距或等比的数据,但总体不呈正态分布,计算它们的相关系数时应选用()A.积差相关B.斯皮尔曼等级相关C.二列相关D.点二列相关
假设两变量为线性关系,这两变量为等距或等比的数据且均为正态分布,计算它们的相关系数时应选用()A.积差相关B.斯皮尔曼等级相关C.二列相关D.点二列相关
两列正态变量,其中一列是等距或等比数据,另一列被人为地划分为两类。计算它们的相关系数应采用()A.积差相关B.多列相关C.二列相关D.斯皮尔曼等级相关
两列变量中有一列是等距或等比测量数据,且服从正态分布,另一列变量是二分称名变量,计算它们相关系数最恰当的公式是
计算积和关系数时、必须满足一定的条件。下列关于这些件的叙述中,并非必要的是()A.两列数据为连续数据B.两列数据总体方差齐性C.两列数据之间存在线性关系D.两列数据总体各自服从正态分布
两个变量分布都是真正的二分变量,要计算两者之间相关系数,最恰当的方法是A.四分相关B.巾相关C.二列相关D.点二列相关
假设两变量线性相关,两变量是等距或等比的数据,且呈正态分布。计算它们的相关系数时应选用( )A.积差相关B.斯皮尔曼等级相关C.二列相关D.点二列相关
两列变量是等距或等比变量,且服从正态分布,计算它们的相关系数最恰当的方法是A.积差相关B.等级相关C.点二列相关D.双列相关
计算相关系数时,对两列数据都作正态分布要求的方法有A.斯皮尔曼等级相关B.皮尔逊积差相关C.垂系数D.二列相关
两列变量中有一列是等距或等比测量数据,且服从正态分布,另一列变量是二分称名变量,计算它们的相关系数最恰当的方法是A.积差相关B.等级相关C.点二列相关D.二列相关
()是哪种相关系数的计算公式A、积差相关系数B、等级相关系数C、点二列相关系数D、等差相关系数
等级相关适用于以下()情况。A、两列观测数据都是顺序变量数据,或其中一列数据是顺序变量数据,另一列数据是连续变量的数据B、两个连续变量的观测数据,其中有一列或两列数据主要依靠非测量方法进行粗略评估得到C、两个连续变量之间的相关情况D、两个变量中的一个是连续变量,另一个是二分类的称名变量
一列数据为顺序变量数据,另一列数据为连续变量数据,计算其相关系数用()A、积差相关B、等级相关C、点双列相关D、列联相关
已知两列变量均为连续变量,样本容量很小,计算两个变量之间的相关系数最好采用()A、积差相关法B、等级相关法C、点双列相关法D、列联相关法
一列是连续变量数据,另一列是顺序变量数据,计算相关系数时应该运用()A、等级相关B、点双列相关C、积差相关D、列联相关
对相关分析的前提条件来说,错误的是()。A、两变量服从正态分布B、两列变量属于连续变量C、一个是原因变量,一个是结果变量D、两列变量有线性关系
单选题已知两列变量均为连续变量,样本容量很小,计算两个变量之间的相关系数最好采用()A积差相关法B等级相关法C点双列相关法D列联相关法
单选题假设两变量线性相关,两变量是等距或等比的数据,但不呈正态分布,计算它们的相关系数时应选用( )。A积差相关B斯皮尔曼等级相关C二列相关D点二列相关
单选题一列是连续变量数据,另一列是顺序变量数据,计算相关系数时应该运用()A等级相关B点双列相关C积差相关D列联相关
单选题()是哪种相关系数的计算公式A积差相关系数B等级相关系数C点二列相关系数D等差相关系数
单选题一列数据为顺序变量数据,另一列数据为连续变量数据,计算其相关系数用()A积差相关B等级相关C点双列相关D列联相关