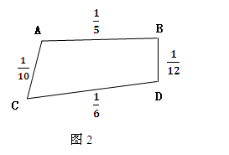
某人从A处开车到D处上班,若各路段发生堵车事件是相互独立的,发生堵车的概率如图2所示(例如路段AC发生堵车的概率是1/10).请选择一条由A到D的路线,使得发生堵车的概率最小,并计算此概率。
某人从A处开车到D处上班,若各路段发生堵车事件是相互独立的,发生堵车的概率如图2所示(例如路段AC发生堵车的概率是1/10).请选择一条由A到D的路线,使得发生堵车的概率最小,并计算此概率。

参考解析
解析:

相关考题:
若事件A发生导致事件B发生,则下列结论成立的是( )。A.事件A发生的概率大于事件B发生的概率B.事件A发生的概率小于事件B发生的概率C.事件B发生的概率等于事件A发生的概率D.事件B发生的概率不小于事件A发生的概率
若事件A发生必然导致事件8发生,则下列结论成立的是( )。A.事件A发生的概率大于事件B发生的概率B.事件A发生的概率小于事件B发生的概率C.事件B发生的概率等于事件A发生的概率D.事件B发生的概率不小于事件A发生的概率
建设工程风险的特点之一是( )。A风险因素的发生概率大,风险事件的发生概率小B风险因素的发 建设工程风险的特点之一是( )。A风险因素的发生概率大,风险事件的发生概率小B风险因素的发生概率小,风险事件的发生概率大C风险因素和风险事件的发生概率均较大D风险因素和风险事件的发生概率均较小
小王需要从①地开车到⑦地,可供选择的路线如下图所示。图中,各条箭线表示路段及其行驶方向,箭线旁标注的数字表示该路段的拥堵率(描述堵车的情况,即堵车概率)。拥堵率=1-畅通率,拥堵率=0时表示完全畅通,拥堵率=1时表示无法行驶。根据该图,小主选择拥堵情况最少(畅通情况最好)的路线是( )。A.①②③④⑤⑦ B.①②③④⑥⑦ C.①②③⑤⑦ D.①②④⑥⑦
下图是一个选择出行路线的“决策树图”,统计路线 1 和路线 2 堵车和不堵车的用时和其发生的概率(P),计算出路线 1 和路线 2 的加权平均用时,根据计算结果选择出行路线。以下结论中,正确的是:()。 A,路线 1 的加权平均用时为 40.5 分钟,路线 2 的加权平均用时为 48 分钟,因此选择路线 1A.路线 1 的加权平均用时为 62.5 分钟,路线 2 的加权平均用时为 40 分钟,因此选择路线2B.路线 1 的加权平均用时为 40.5 分钟,路线 2 的加权平均用时为 44 分钟,因此选择路线1C.由于路线 2 堵车和不堵车时间都比路线 1 短;因此选择路线 2
下列关于概率的说法,错误的有()。A:概率分布是不确定事件发生的可能性的一种数学模型B:如果两个事件不可能同时发生,那么至少其中之一发生的概率为这两个概率的积C:当随机事件A的结果不影响随机事件B发生的概率时,则称两个事件是独立的D:如果两个事件是相互独立的,那么这两个事件同时发生的概率就是这两个事件各自发生的概率的和E:一些概率既不能由等可能性来计算,也不可能从试验得出,需要根据常识、经验和其他相关因素来判断,这种概率称为主观概率
关于事件A的概率,叙述正确的有( )。A:由于频率总介于0与1之间,故随机事件A的概率也总是介于0与1之间B:若A为必然事件,则其概率是1C:若A为不可能事件,则其概率是0D:若事件A在10次试验中发生10次,则事件A的概率为1E:若A为小概率事件,通常认为在一次试验中A几乎不可能发生
小王需要从①地开车到⑦地,可供选择的路线如下图所示。图中,各 条箭线表示路段及其行驶方向,箭线旁标注的数字表示该路段的拥堵 率(描述堵车的情况,即堵车概率)。拥堵率=1-畅通率,拥堵率=0 时表示完全畅通,拥堵率=1时表示无法行驶。根据该图,小主选择拥 堵情况最少(畅通情况最好)的路线是( )。A. ①②③④⑤⑦B. ①②③④⑥⑦C. ①②③⑤⑦D. ①②④⑥⑦
某人从A处开车到D处上班,若各路段发生堵车事件是相互独立的,发生堵车的概率如图2所示(例如路段AC发生堵车的概率是l/10)。请选择一条由A到D的路线.使得发生堵车的概率最小,并计算此概率。
下图是一个选择出行路线的“决策树图”,统计路线1和路线2堵车和不堵车的用时和其发生的概率(P),计算出路线1和路线2的加权平均用时,根据计算结果选择出行路线。以下结论中,正确的是( ) 。 A.路线1的加权平均用时为4 0.5分钟,路线2的加权平均用时为4 8分钟,因此选择路线1 B.路线1的加权平均用时为6 2.5分钟,路线2的加权平均用时为4 0分钟,因此选择路线2 C.路线1的加权平均用时为4 0.5分钟,路线2的加权平均用时为4 4分钟,因此选择路线1 D.由于路线2堵车和不堵车时间都比路线1短;因此选择路线2
以下关于概率的说法,正确的有()。A、如果两个事件不可能同时发生,那么至少其中之一发生的概率为这两个概率的积B、概率分布是不确定事件发生的可能性的一种数学模型C、如果两个事件相互独立的,那么这两个事件同时发生的概率就是这两个事件各自发生的概率的和D、当我们知道A的结果不影响B发生的概率时,我们就说两个事件就概率而言是独立的E、一些概率既不能由等可能性来计算,也不可能从试验得出,需要根据常识、经验和其他相关因素来判断,这种概率称为主观概率
单选题设两个相互独立的事件A和B都不发生的概率为1/9,A发生B不发生的概率与B发生A不发生的概率相等,则P(A)=( )。A1/9B2/3C1/3D1/6