当前股价为15元,一年后股价为20元或10元,无风险利率为6%,计算剩余期限为1年的看跌期权的价格所用的无风险中性概率为()。(参考公式A、0.59B、0.65C、0.75D、0.5
当前股价为15元,一年后股价为20元或10元,无风险利率为6%,计算剩余期限为1年的看跌期权的价格所用的无风险中性概率为()。(参考公式
A、0.59
B、0.65
C、0.75
D、0.5

A、0.59
B、0.65
C、0.75
D、0.5
参考解析
解析:根据已知条件,可得u=20/15=4/3;d=10/15=2/3,代入计算公式,可得:
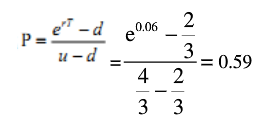
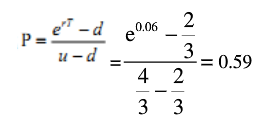
相关考题:
甲公司股票当前每股市价为80元,6个月以后,股价有两种可能:上升25%或下降20%。市场上有两种以该股票为标的资产的期权:看涨期权和看跌期权。每份看涨期权可买入1股股票,每份看跌期权可卖出1股股票;两种期权执行价格均为85元,到期时间均为6个月;期权到期前,甲公司不派发现金股利,年无风险利率为6%。要求:?、利用套期保值原理,计算看涨期权的股价上行时到期日价值、套期保值比率及期权价值,利用看涨期权—看跌期权平价定理,计算看跌期权的期权价值。?、假设市场上每份看涨期权价格6.5元,每份看跌期权价格8.5元,投资者同时卖出一份看涨期权和一份看跌期权,计算确保该组合不亏损的股票价格区间;如果6个月后的标的股票价格实际上涨20%,计算该组合的净损益。(注:计算股票价格区间和组合净损益时,均不考虑期权价格的货币时间价值)。
甲公司股票当前每股市价40 元,6 个月以后股价有两种可能,上升25%或下降20%,市场上有两种以该股票为标的资产的期权:看涨期权和看跌期权,每份看涨期权可以买入1 股股票,每份看跌期权可以卖出1 股股票,两种期权执行价格均为45 元,到期时间均为6 个月,期权到期前,甲公司不派发现金股利,半年无风险报酬率为2%。要求:(2)假设市场上每份看涨期权价格为2.5 元,每份看跌期权价格1.5 元,投资者同时卖出一份看涨期权和一份看跌期权,计算确保该组合不亏损的股票价格区间,如果6 个月后的标的股票价格实际上涨20%,计算该组合的净损益。(注:计算股票价格区间和组合净损益时,均不考虑期权价格的货币时间价值)。(2)利用风险中性原理,计算看涨期权的股价上行时到期日价值、上行概率及期权价值,利用看涨期权—看跌期权平价原理,计算看跌期权的期权价值。
假设A公司目前的股票价格为20元/股,有1股以该股票为标的资产的看涨期权,到期时间为6个月,执行价格为24元, 6个月内公司不派发股利,预计半年后股价有两种可能,上升30%或者下降23%,半年的无风险利率为4%。 要求:(1)用复制原理计算该看涨期权的价值。 (2)用风险中性原理计算该看涨期权的价值。 (3)如果该看涨期权的现行价格为2.5元,请根据套利原理,构建一个投资组合进行套利。
(2015年)甲公司股票当前每股市价40 元,6 个月以后股价有两种可能,上升25%或下降20%,市场上有两种以该股票为标的资产的期权:看涨期权和看跌期权,每份看涨期权可以买入1 股股票,每份看跌期权可以卖出1 股股票,两种期权执行价格均为45 元,到期时间均为6 个月,期权到期前,甲公司不派发现金股利,半年无风险报酬率为2%。要求:(1)假设市场上每份看涨期权价格为2.5 元,每份看跌期权价格1.5 元,投资者同时卖出一份看涨期权和一份看跌期权,计算确保该组合不亏损的股票价格区间,如果6 个月后的标的股票价格实际上涨20%,计算该组合的净损益。(注:计算股票价格区间和组合净损益时,均不考虑期权价格的货币时间价值)。(2)利用风险中性原理,计算看涨期权的股价上行时到期日价值、上行概率及期权价值,利用看涨期权—看跌期权平价原理,计算看跌期权的期权价值。
假设某欧式看涨期权目前股价为4.6元,期权的行权价为4.5元,期限为1年,股价年波动率为0.3,无风险利率为6%,则该看涨期权的价值为()元。(已知累积正态分布表N(0.42)=0.6628,N(0.12)=0.5478) A、0.96B、0.54C、0.66D、0.72
标的资产为不支付红利的股票,当前价格为 30 元,已知 1 年后该股票价格或为 37.5 元,或为 25 元,风险中性概率为 0.6。假设无风险利率为 8%,连续复利,计算对应 1 年期,执行价格为 25 元的看涨期权理论价格为( )元。A.6.92B.7.23C.6.54D.7.52
6 个月后到期的欧式看涨期权价格为 5元,标的现货价格为 50 元,执行价格为 50 元,无风险利率为 5%。根据期权平价公式,其对应的欧式看跌期权价格为( )元。A.3.76B.3.63C.2.99D.4.06
6个月后到期的欧式看涨期权价格为5元,标的资产价格为50元,执行价格为50元,无风险利率为5%,根据期权定价公式,某对应的欧式看跌期权价格为( )元。A: 2.99B: 3.63C: 4.06D: 3.76
假设2个月到期的欧式看跌期权价格为2.5美元,执行价格为50美元,标的股票当前价格为46美元,设无风险利率为6%,股票无红利,则以下如何操作可以无风险套利()A、买入股票、买入期权B、买入股票、卖出期权C、卖出股票、买入期权D、卖出股票、卖出期权
某货币的当前汇率为0.56,汇率波动率为15%,国内无风险利率为年率5%,外国无风险利率年率为8%,则根据货币期权的定价模型,期权执行价格为0.5的6个月期欧式货币看跌期权价格为()美元。A、0.005B、0.0016C、0.0791D、0.0324
一个无股息股票的美式看涨期权的价格为3美元。股票当前价格为21美元,执行价格为20美元,到期期限为3个月,无风险利率为6%。则对于相同标的股票、相同执行价格和相同到期期限的美式看跌期权,以下表述正确的是()。A、该期权的上限为1.3美元B、该期权的上限为2.0美元C、该期权的下限为1.0美元D、该期权的下限为1.7美元
假设股票现在的价格为100元,不支付股利,以3个月为一期,3个月内股价可能上涨到原来的1.2倍,也可能下降到原来的0.8倍,无风险利率为12%(连续复利)。试求6个月后到期的执行价格为110元的美式看跌期权的价格。
ABC公司的股票目前的股价为10元,有1股以该股票为标的资产的欧式看涨期权,执行价格为10元,期权价格为2元,到期时间为6个月。假设年无风险利率为4%,计算1股以该股票为标的资产、执行价格为10元、到期时间为6个月的欧式看跌期权的价格;
单选题某货币的当前汇率为0.56,汇率波动率为15%,国内无风险利率为年率5%,外国无风险利率年率为8%,则根据货币期权的定价模型,期权执行价格为0.5的6个月期欧式货币看跌期权价格为()美元。A0.005B0.0016C0.0791D0.0324
问答题ABC公司的股票目前的股价为10元,有1股以该股票为标的资产的欧式看涨期权,执行价格为10元,期权价格为2元,到期时间为6个月。假设年无风险利率为4%,计算1股以该股票为标的资产、执行价格为10元、到期时间为6个月的欧式看跌期权的价格;
单选题假设某欧式看涨期权目前股价为4.6元,期权的行权价为4.5元,期限为1年,股价年波动率为0.3,无风险利率为6%,则该看涨期权的价值为()元。(已知累积正态分布表N(0.42)=0.6628,N(0.12)=0.5478)A0.96B0.54C0.66D0.72
单选题一份看跌期权的标的资产为不分红的股票,合约有效期为120天。当前股价为47美元/股,无风险利率为5%。如果执行价格为50美元,那么美式看跌期权和欧式看跌期权的价格下限分别为( )。A2.2美元,2.2美元B2.2美元,3.0美元C3.0美元,2.2美元D3.0美元,3.0美元E3.0美元,3.2美元
单选题考虑一个欧式看涨期权,其标的资产为不分红的股票。目前股价为100美元/股,执行价格为102美元/股,期权期限为9个月,无风险利率为7.25%。该期权价格的下限为( )美元。A0B2.136C3.216D3.963E4.123
问答题甲公司股票当前每股市价40元,6个月以后股价有两种可能:上升25%或下降20%,市场上有两种以该股票为标的资产的期权:看涨期权和看跌期权。每份看涨期权可买入1股股票,每份看跌期权可卖出1股股票,两种期权执行价格均为45元,到期时间均为6个月,期权到期前,甲公司不派发现金股利,半年无风险报酬率为2%。利用风险中性原理,计算看涨期权的股价上行时到期日价值、上行概率及期权价值,利用看涨期权一看跌期权平价定理,计算看跌期权的期权价值。
问答题假设A公司目前的股票价格为20元/股,以该股票为标的资产的看涨期权到期时间为6个月,执行价格为24元,预计半年后股价有两种可能,上升30%或者下降23%,半年的无风险利率为4%。要求: (1)用复制原理计算该看涨期权的价值; (2)用风险中性原理计算该看涨期权的价值; (3)如果该看涨期权的现行价格为2.5元,请根据套利原理,构建一个投资组合进行套利。
单选题当前股价为15元,一年后股价为20元或10元,无风险利率为6%,计算剩余期限为1年的看跌期权的价格所用的无风险中性概率为()。A0.59B0.65C0.75D0.5