初中数学《勾股定理》
一、考题回顾
题目来源1月6日 下午 黑龙江省哈尔滨市 面试考题
试讲题目1.题目：勾股定理
2.内容：



3.基本要求：
(1)要有板书;
(2)试讲十分钟左右;
(3)条理清晰，重点突出;
(4)学生掌握勾股定理的证明方法。
答辩题目1.勾股定理的教学过程中，体现了什么数学思想?
2.常见的三组勾股数是什么?
二、考题解析
【教学过程】
(一)引入新课
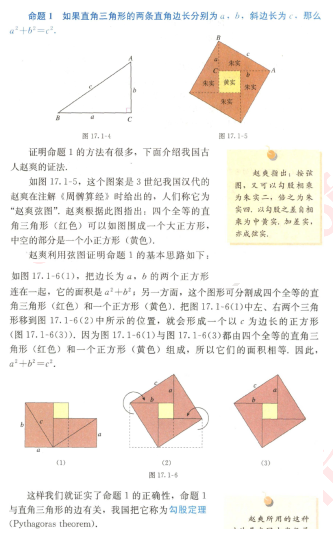
出示“国际数学家大会会徽”，提出问题：会徽图案有什么特别的含义吗?蕴含什么样的数学奥秘?
(二)探索新知
活动1：出示“毕达哥拉斯朋友家地板砖图”。
?


引导学生发现理解图形中全等的直角三角形的某种数量关系，并提出问题：等腰直角三角形三边长具有怎样的关系?引导学生利用面积规律整理归纳得出：等腰直角三角形两条直角边的平方和等于斜边的平方。
问题1：一般的直角三角形是否也具有类似规律?引导学生在网格图利用面积探究规律并归纳出：直角三角形两条直角边的平方和等于斜边的平方。

答案：

解析：

《勾股定理》
一、面试考题
试讲题目
1.题目：勾股定理
2.内容：

3.基本要求：
(1)试讲时间10分钟;
(2)讲解要目的明确、条理清楚、重点突出;
(3)根据讲解的需要适当板书;
(4)学生掌握勾股定理的证明方法。
答辩题目
1.勾股定理还有哪些证明方法?
2.本节课的设计思路是什么?
注：图片节选自人民教育出版社初中数学八年级下册第23-24页

答案：

解析：

二、考题解析
【教学过程】
(一)导入新课
复习导入：复习三角形三边关系，说明直角三角形中三边存在着更特殊的数量关系，引出课题《勾股定理》。
(二)讲解新知

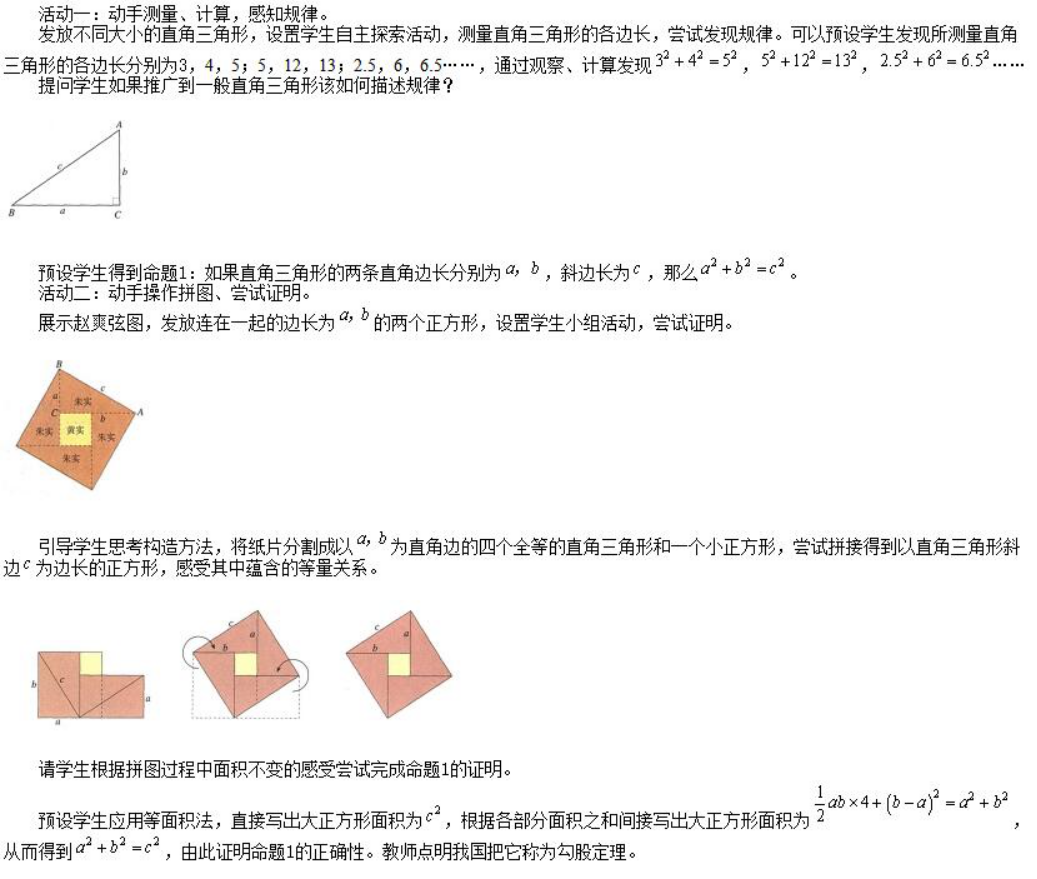
(三)课堂练习
已知直角三角形的两边长为3和4，求第三边。
(四)小结作业
小结：提问学生本节课有哪些收获。
作业：搜集勾股定理的数学小典故，第二天分享交流。
【板书设计】

一、考题回顾
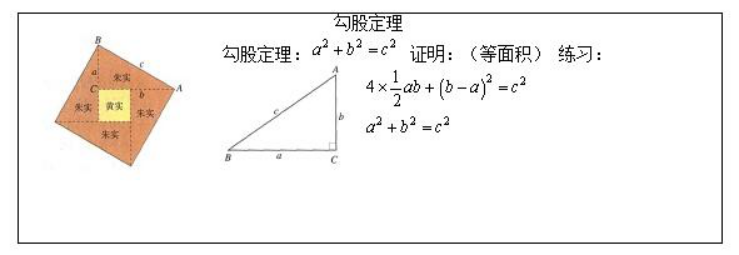
题目来源：1月6日上午河南省安阳市面试考题
试讲题目：初中数学《勾股定理》

3基本要求:
(1) 要有板书;
(2) 试讲十分钟左右;
(3) 条理清晰，重点突出;
(4 )学生掌握勾股定理的证明方法。
答辩题目
1.勾股定理的教学过程中，体现了什么数学思想?
2.常见的三组勾股数是什么?

答案：

解析：

北师大版八年级上勾股定理学案 一教学目标： 1. 经历勾股定理及直角三角形判别条件（逆定理）的探索，了解勾股定理的各种探究方法及其内在联系，进一步发展学生的推理。 它们的应用。 二知识要点 ： 1.。 勾股定理：如果直角三角形两直角边分别为 a、 b，斜边为 c，那么 a2+b2=直角三角形两直角边的平方和等于斜边的平方 （由直角三角形得到边的关系） 2. 勾股定理逆定理： 如果三角形的三边长 a， b， ，那么这个三角形是直角三角形。 的三个正整数，称为勾股数。 常见的勾股数组有：（ 3， 4， 5）；（ 6， 8， 10）；（ 5，12， 13）；（ 8， 15， 17）；（ 7， 24， 25）；（ 20， 21， 29）；（ 9， 40， 41）；（这些勾股数组的倍数仍是勾股数） 【一】勾股定理的验证与证明 个小正方形的边长是 1，图中三个正方形的面积分别是 它们的面积关系是 ，直角 三边的关系是 . 由四个全等的 成的图形，你能用它证明勾股定理吗？ 是由四个全等的 成的图形，你能用它证明勾股定理吗？ 知 A B 90且 A、 E、 根据此图证明勾股定理 . 【二】勾股定理的简单运用 根据所标数据，确定正方形的面积 A ， B ， C . 1a 线 l 上有三个正方形 a、 b、 c 若 a 和 c 的面积分别为 5 和 11，则 b 的面积为多少？ 直角三角形的三边向形外作等边三角形，探究 直 角三角形的三边向形外作等腰直角三角形，探究 5. 如图，以直角三角形的三边向形外作半圆， 探究 6. 如图，已知 ， 90，以 各边为长边向形外作矩形，使其宽为长的一半，则这三个矩形的面积 证明你的结论 . 7. 如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形边长为 7正方形 A、 B、C、 D 的面积之和为多少？ 水平面上依次放 置着七个正方形已知斜放置的三个正方形的面积分别是 a、 b、 c，正放置的四个正方形的面积依次是 则 . 【三】利用勾股定理求边长 t ， C 90， a 12， b 16，则 c 的长为（ ） 知点 P 的 坐标是 (3,4)，则 长为（ ） D. 7 3将直角三角形的三边扩大相同的倍数后，得到的三角形是（ ） A 直角三角形 B 锐角三角形 C 钝角三角形 D 不能确定 ，则该三角形的面积为（ ） A. 43 B. 3 C. 23 0，底边长为 12，则底边上的高为（ ） 、 4、 x，则使此三角形是直角三角形的 x 的值是（ ） B. 6 C. 7 7 a， b， c 为边的三角形不是 是（ ） ， b=3, c=4 , b=24, c=25 , b=8, c=10 , b=4, c=5 m 处向地面拉一条长为 1

初中数学《勾股定理的逆定理》
一、考题回顾

答案：

解析：

二、考题解析
【教学过程】
(一)引入新课
引导学生复习勾股定理，并向学生提问：怎么画一个直角三角形?
预设：用三角尺。
提问：如果不用三角尺，怎么画直角三角形?并给学生出示古埃及人画直角三角形的情景，并引导学生思考：其中蕴含着什么规律呢?进而引出课题。
(二)探索新知
对于导入中的问题，教师可先引导学生思考3，4，5有什么样的关系?预设：32+42=52。
再继续出示几组数据：2.5，6，6.5以及4，7.5，8.5引导学生采用尺规作图。并观察做出的三角形的形状。
引导学生大胆猜想，得到：如果三角形的三边长分别为a，b，c，满足a2+b2=c2，那这个三角形就是一个直角三角形。
提问：那怎么证明这个猜想是正确的?
引导学生采用尺规作图的方式，做出和已知三角形三边相同的直角三角形，利用勾股定理得出三角形的对应的三边相等，进而两个三角形全等，也就证明上述的猜想是正确的。
引导学生观察勾股定理和命题2，说说两个命题有什么样的关系?
预设：两个命题的条件和结论是相反。
进而给出原逆命题的概念。并给说明上述的发现也是一个定理，称为勾股定理的逆定理。
提问：原命题正确，逆命题一定正确?
预设：对顶角相等，但是两个角相等，不一定是对顶角。
最后，师生共同得出：原命题正确，逆命题不一定正确，只有正确的逆命题才能叫做原命题的逆定理。
(三)课堂练习
判断由线段a，b，c组成的三角形是不是直角三角形。
(1)a=15，b=8，c=17;(2)a=13，b=14，c=15。
(四)小结作业
提问：今天有什么收获?
课后作业：课后作业1-3。
【板书设计】




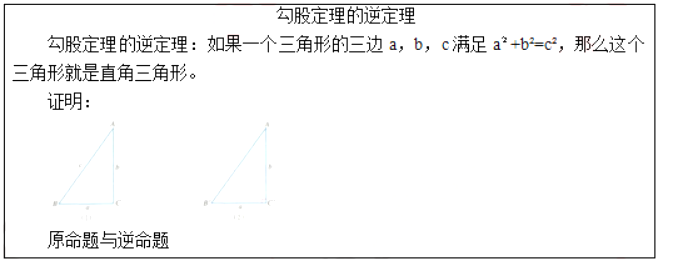
【答辩题目解析】
1.谈一谈勾股定理在初中教材中的地位?
【参考答案】
勾股定理是初中几何中几个重要定理之一。它揭示了直角三角形三边的某种数量关系。勾股定理是建立在三角形、全等三角形、等腰三角形等有关知识的基础之上，同时也是初三几何中解直角三角形及圆中有关计算的必备知识。更重要的是，纵观整个初中数学，勾股定理架起了代数与几何之间的桥梁。勾股定理在数学理论体系中的地位举足轻重，在日常生活、工农业生产中，应用极为广泛。就学生而言，对勾股定理学习的好坏将直接影响到他们后续数学的学习。
2.教学过程中你主要设置了哪些问题，目的是什么?
【参考答案】
第一个问题：把一根长绳打上13个绳结，以3、4、5个结间距为边长组成的三角形中就有一个是直角。用这样的绳结组成的三角形是直角三角形么?
设计意图：通过这样的古代数学问题激发学生的学习兴趣，从而引出本节课的课题《勾股定理的逆定理》。
第二个问题：动手操作导入问题以及2.5，6，6.5;6，8，10能否组成直角三角形?根据以上结论能得出什么猜想?
设计意图：鼓励学生动手探究提升综合实践能力，进一步根据事实作出猜想提升合情推理能力。
第三个问题：这个命题正确么?
设计意图：鼓励学生对猜想进行证明养成良好的反思质疑的学习习惯并进一步提升演绎推理能力。

设的三条边分别是a，b，C，且a2+b2=c2。证明：ΔABC是直角三角形。(这是勾股定理的逆命题)

答案：

解析：

证明．以n．b长为直角边作Rt△A，B，C．设斜边长为d．则由勾股定理得

全等．故ABC是直角三角形。

数学课上，黄老师在讲勾股定理时，先给学生讲明勾股定理的内容，然后再讲述推导证明过程。黄老师所采用的教学方法是（）。

• A、讨论式
• B、逆推式
• C、带动式
• D、导入式

• 理学
• 压路机资格考试
• 第十六章 诱发电位
• 算法设计与分析
• 临床营养学
• 物业管理师
• 设备安装质量员质检员
• 人防工程监理
• 肿瘤内科学相关专业知识
• 水利工程检测员继续教育
• 焙烧工考试
• 广东住院医师儿科学
• 专业能力
• 北京住院医师麻醉科
• 职称英语
• 湖北住院医师神经外科
• 住院医师公共科目
• 天车工考试
• 电力线路工
• 成品油物流优化管理考试