福建师范大学22春《复变函数》在线作业二及答案参考12
设曲线y=f(x)上任一点(x,y)处的切线斜率为(y/x)+x2,且该曲线经过点(1,1/2)。
(1)求函数y=f(x);
(2)求由曲线y= f(x),y=O,x=1所围图形绕x轴旋转一周所得旋转体的体积V。
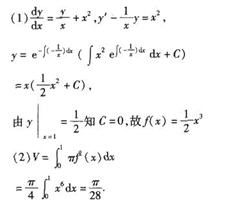
如题6-2图所示电路中,开关S接在1处时电路已达稳态,在t=0时,S由1接至2。求换路后的电流iL(t)、电压uL(t),并绘出它们的变化曲线。
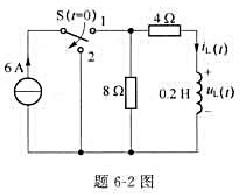


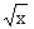 ,直线z=1和z轴所围成的有界平面图形的面积s,及该平面图形绕2轴旋转一周所得旋转体的体积V.
,直线z=1和z轴所围成的有界平面图形的面积s,及该平面图形绕2轴旋转一周所得旋转体的体积V.
①求由曲线C与直线L所围成的平面图形的面积S;
②求曲线C的平行于直线L的切线方程.
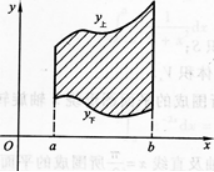
图1—3—3

图1—3—4
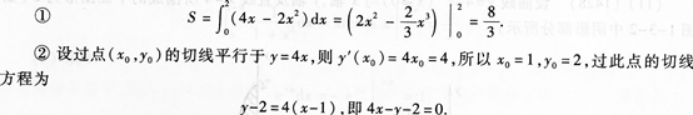
①求曲线y=(x)与x轴所围成的平面图形面积S;
②求①的平面图形绕x轴旋转一周所得旋转体体积Vx.

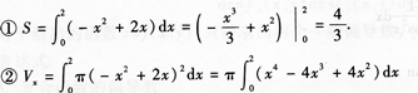
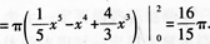
福建师范大学22春复变函数在线作业二及答案参考1. (x-c)2+(y-c)2=4 求曲线族的包络,并绘出图形:(x-c)2+(y-c)2=4 求曲线族的包络,并绘出图形:由(x-c)2+(yc)2=4,2c=x+y,得(x-y)2=8 见图3.14 2. 设f(x)在x=x0的附近二阶连续可导,f&39;(x0)=0,f(x0)0,则f(x)在x=x0处有( ) (A) 极大值 (B) 极设f(x)在x=x0的附近二阶连续可导,f(x0)=0,f(x0)0,则f(x)在x=x0处有()(A)极大值(B)极小值(C)拐点(D)既非极值点也非拐点B根据洛必达法则, 说明当x充分接近x0时,f(x)-f(x0)0即x=x0是f(x)的极小值点 3. 拟完美序列的周期自相关函数的的旁瓣值都等于多少?A、0.0B、2.0C、1.0D、2.0拟完美序列的周期自相关函数的的旁瓣值都等于多少?A、0.0B、2.0C、-1.0D、-2.0正确答案: C4. 求n=1+(n+2)xn+3的和函数求n=1+(n+2)xn+3的和函数5. 设数列un为等差数列,un0(n=1,2,.),证明:级数是发散的设数列un为等差数列,un0(n=1,2,.),证明:级数是发散的设u1=a,un=u1+nd=a+nd,其中d为公差,则当un0时,有 不妨设公差d0,可知必定存在N,使a+Nd0,因而当nN时,(如果d0,必定存在N,使a+Nd0,因而当nN时,) 由于,且当d0时有 由正项级数极限形式的比较判别法可知: 当nN时,a+nd0时,发散,若当nN时,a+nd0,发散,因此不论a+nd0还是a+nd0,可知发散只需写出un的一般表达式可解 6. 假设目标出现在射程之内的概率为0.7,这时射击命中目标的概率为0.6,试求两次独立射击至少有一次命中目标的概假设目标出现在射程之内的概率为0.7,这时射击命中目标的概率为0.6,试求两次独立射击至少有一次命中目标的概率p0.5887. 2一平面经过原点和另一点(6,3,2)且与平而5x+4y-3z=8垂直,求此平面方程。2一平面经过原点和另一点(6,3,2)且与平而5x+4y-3z=8垂直,求此平面方程。2-17x+28y+9=08. 求下面微分方程的通解或特解。y=1+(y&39;)2求下面微分方程的通解或特解。y=1+(y)2设y=p(x),则y=p(x),将y=p(x)、y=p(x)代入原方程中,有 p=1+p2 分离变量,得 两边积分,得 arctanp=x+c1 p=tan(x+c1) y=p=tan(x+c1) 9. 试证明: 设f(x)在0,)上非负可积,f(0)=0且f&39;(0)存在,则存在积分 试证明:设f(x)在0,)上非负可积,f(0)=0且f(0)存在,则存在积分证明 因为我们有,所以对任给0,存在0,使得 0f(x)/xf(0)+ (0x) 由此知f(x)/x在0,上可积,且从不等式 , 可知f(x)/x在,)上可积,证毕 10. 某年级三个班,进行了一次数学考试,从各班随机抽取部分学生,记录其数学成绩如下表所示: 1班 2班某年级三个班,进行了一次数学考试,从各班随机抽取部分学生,记录其数学成绩如下表所示:1班2班3班73668960887778314887684179598245938078916251767156689l53367743738596748056797115试在显著性水平=0.05下检验各班成绩有无显著差异设各总体是正态总体,且方差相等以i记第i班平均成绩(i=1,2,3),待检假设H0:1=2=3 s=3,n1=12,n2=15,n3=13,n=40, SE=ST-SA=13349.75,列出方差分析表如下: 方差来源 平方和 自由度 均方 F比 结论 因素 335.35 2 167.675 0.4647 不显著 误差 13349.75 37 360.80 总和 13685.1 39 F0.05(2,37)=3.23F比=0.4647,故拒绝H0,认为各班成绩无显著差异 11. 设区域D为:由以点为顶点的四边形与以点, 为顶点的三角形合成,随机变量(X,Y)在D上服从均匀分布,求关于X、Y的设区域D为:由以点为顶点的四边形与以点,为顶点的三角形合成,随机变量(X,Y)在D上服从均匀分布,求关于X、Y的边缘概率密度12. 已知(2x)x2a(x1)b(x1)2(x1),求a,b的值。已知(2x)x2a(x1)b(x1)2(x1),求a,b的值。正确答案:解 令 x1tx1t0rn解令x1t,x1,t013. 我国关于对圆周率 的计算,贡献最大的人物是:A、杨辉B、张衡C、刘徽D、祖冲之我国关于对圆周率 的计算,贡献最大的人物是:A、杨辉B、张衡C、刘徽D、祖冲之正确答案: D14. 2xydy=(2y2x)dx2xydy=(2y2-x)dx15. 设随机变量X的分布函数求其概率密度,且求P(X1)设随机变量X的分布函数求其概率密度,且求P(X1) 16. 证明:当n3时,全体3一循环是交代群An的一个生成系证明:当n3时,全体3一循环是交代群An的一个生成系正确答案:n=3时结论显然成立因此下设n3rn 由于An中每个元素都可表为偶数个对换之积从而也就是一些形如rn (ab)(cd)或(ab)(ac)的项之积其中abcd是12n中互异的元素但由于rn (ab)(cd)=(abc)(bcd) (ab)(ac)=(acb)rn故An中的每个元素又都是一些3一循环之积即An由全体3一循环生成n=3时,结论显然成立因此下设n3由于An中每个元素都可表为偶数个对换之积,从而也就是一些形如(ab)(cd)或(ab)(ac)的项之积其中a,b,c,d是1,2,n中互异的元素但由于(ab)(cd)=(abc)(bcd),(ab)(ac)=(acb),故An中的每个元素又都是一些3一循环之积,即An由全体3一循环生成17. 设某养老金计划参加者具体的存款方式为:在2529岁时,每月存款200元;在3039岁时,每月存款300元;在4049岁时设某养老金计划参加者具体的存款方式为:在2529岁时,每月存款200元;在3039岁时,每月存款300元;在4049岁时,每月存款500元;在5059岁时,每月存款1000元在年利率i=10%下,分别对不同年龄的计划参加者计算月退休金年利率i=10%,因此有,=271.0244, (1)恰好在25岁开始加入养老金计划,则60岁以后的月退休金为 即每月领取约10580元的退休金,直至80岁 (2)从30岁开始加入养老金计划,则60岁以后的月退休金为 即每月领取约8078元的退休金,直至80岁 (3)从40岁开始加入养老金计划,则60岁以后的月退休金为 即每月领取约4300元的退休金,直至80岁 18. 计算mod5的整数的加法表、乘法表和减法表。计算mod5的整数的加法表、乘法表和减法表。 oplus 0 1 2 3 4 0 0 1 2 3 4 1 1 2 3 4 0 2 2 3 4 0 1 3 3 4 0 1 2 4 4 0 1 2 3 otimes 0 1 2 3 4 0 0 0 0 0 0 1 0 1 2 3 4 2 0 2 4 1 3 3 0 3 1 4 2 4 0 4 3 2 1 ominus 0 1 2 3 4 0 0 4 3 2 1 1 1 0 4 3 2 2 2 1 0 4 3 3 3 2 1 0 4 4 4 3 2 1 0 19. 求通过坐标原点,与曲面x2-2yz-2y+4z-3=0相切而且与直线相交的直线方程求通过坐标原点,与曲面x2-2yz-2y+4z-3=0相切而且与直线相交的直线方程设所求直线方程为 因为所求直线与相交,所以 即X-Y+Z=0且X:Y:Z2:1:(-1), 令,则有 x=tX,y=tY,z=tZ,代入曲面方程得 (tX)2-2t2YZ+2tY+4tZ-3=0, 即(X2-2YZ)t2-(2Y-4Z)t-3=0,因为直线与曲面相切,所以 (2Y-42)2+12(X2-2YZ)=0, 即Y2-4YZ+4Z2+3X2-6YZ=0, 由得X=Y-Z, 代入得Y2-10YZ+4Z2+3(Y-Z)2=0, 即4Y2-16YZ+7Z2=0, 即(2Y-7Z)(2Y-Z)=0, 所以2Y=7Z或2Y=Z, 当2Y=7Z时, 当2Y=Z时, 所以求得X:Y:2=5:7:2或X:Y:Z=(-1):1:2, 故所求直线方程为 与 20. 设函数,f&39;(x)连续,且f(0)=0设函数,f(x)连续,且f(0)=0A=0时,F(x)在x=0处连续$当x0时,而 又 故F(x)在x=0处连续 21. 任放一张红牌或黑牌,让A看但不让B知道。如是红牌,A可以掷一枚硬币或让B猜,掷硬币出现正反面概率各为12,出现任放一张红牌或黑牌,让A看但不让B知道。如是红牌,A可以掷一枚硬币或让B猜,掷硬币出现正反面概率各为1/2,出现正面,A赢得p元,出现反面,A输q元;如让B猜,B猜红,A输r元,猜黑,A赢s元。如是黑牌,A只能让B
②求①中的平面图形绕x轴旋转一周所得旋转体的体积V.

②求①中的平面图形绕Y轴旋转一周所得旋转体的体积Vy.
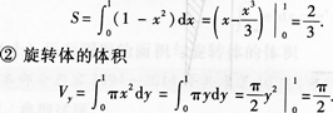
图1—3—5
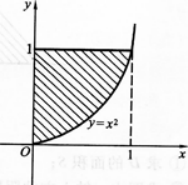
②求①中的平面图形绕x轴旋转一周所得旋转体的体积Vx.
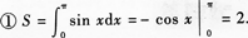
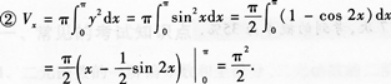
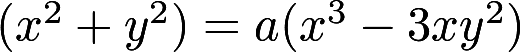 , (a > 0)
, (a > 0)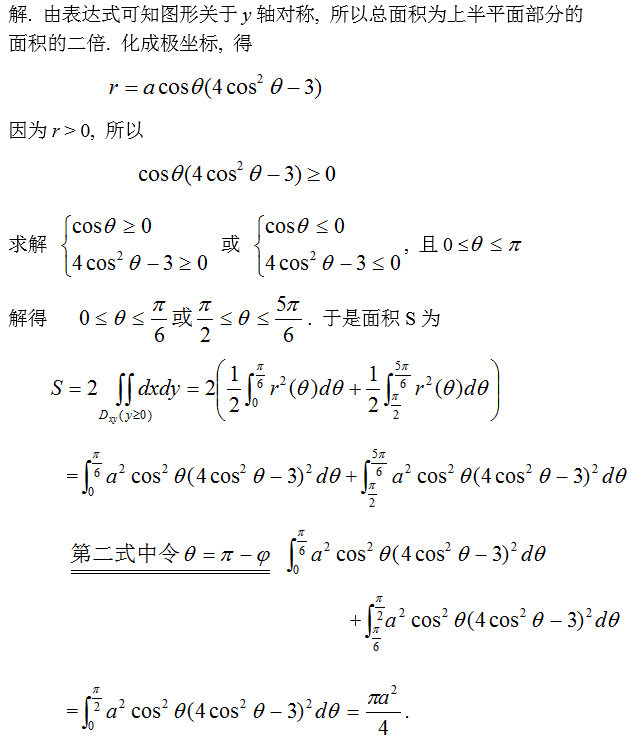
 , (I)求L的弧长; (II)设D是由曲线L,直线x=1,x=e及x轴所围平面图形,求D的形心的横坐标
, (I)求L的弧长; (II)设D是由曲线L,直线x=1,x=e及x轴所围平面图形,求D的形心的横坐标

相关考题:
- 贷款损失准备的计提,不论是本币资产还是外币资产,必须以人民币计提。
- 商业汇票的付款人是持票人。
- 根据弗罗姆的期望理论,员工对一旦完成任务就可以获得报酬的信念称为( )。 A。效价 B。期望 C.工具 D.动机
- 国防是一个庞大的系统工程,国防强固必须优化各相关要素,包括( )、( )、( )、( )、( )、( )、( )、( )。A.政治清明,经济实力雄厚B.武装力量强大C.全民爱国,关心国防D.实行进攻性的军事战略E.国防科技工业先进配套F.国防工程设施完善G.建立广泛的国际联盟H.国防动员体制机制先进有效
- ( 难度:中等)Hive与传统关系型数据库对比,优势有A.计算能力更强B.延迟更低C.扩展性更好D.索引各类更多
- ( 难度:中等)关于参数传递说法正确的()A.A:基本数据类型参数传递的是值,引用数据类型参数传递的是引用B.B:不管是基本数据类型还是引用数据类型都是值传递C.C:基本数据类型参数传递的是数据值,引用数据类型参数传递的是对象D.D:基本数据类型参数是值传递,引用数据类型传递是引用传递
- 金融行业的所有资产都是金融资产。
- ( 难度:中等)Kafka消费者偏移量有几种控制方法A.自动提交B.半自动提交C.手动提交D.随机提交
- 单位活期存款的计息时间一般为每月末30日,结算出来的利息于次日入账。
- 刘先生是某广告公司设计部的主管,他发现手下员工的士气普遍比较低落,工作业绩也一直没有起色。刘先生在员工中进行了调查,结果发现员工普遍感觉工作内容十分枯燥,每天只能按部就班地完成上面分配下来的工作,缺乏成就感.针对这种情况,为了调动员工的积极性,刘先生决定在设计部每月评选一名工作出色的员工,并给予重奖;但是这项措施实行一段时间之后,情况没有任何改观;有员工表示,每月优秀员工的评选缺乏客观的指标,无法反映个人的真实工作情况。 根据赫兹伯格的双因素理论,设计部员工所关注的是( )。 A。保健因素 B.激励因素 C。工资因素 D.安全因素