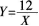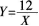投两颗骰子,面朝上的点数之和为8的概率是( )。A. 1/6B. 5/36C. 1/9D. 1/13
将一枚硬币反复向上抛n次,以x和y分别表示正面朝上和反面朝上的次数,则x和y之间的相关系数是()。 A. -1B.0C.1/2D.1
双曲线x2-y2/2 =1在点(-√2,√2)处的切线的方程是( ).(A)y=-x+√2.(B)y=-x+3√2.(C)y=-2x-√2.(D)y=-2x+3√2.
假设有单精度浮点数x和y,x为正有限值,y为正无限值,下列说法中正确的是 ______。A.x/y为NaNB.x/y为负无限C.x/y为正无限D.x/y为0.0
现在有负无限值双精度浮点数x和负有限值单精度浮点数y,以下关于x%y的说法中,______是正确的。A.NaNB.负无限双精度浮点数C.负有限双精度浮点数D.负无限单精度浮点数
质地均匀的骰子六面分别刻有1-6的点数,掷两次骰子,得到向上一面的两个点数,则下列事件中,发生可能性最大的是()。A.点数都是偶数B.点数的和为奇数C.点数的和小于10D.点数的和大于7
投掷一枚质地均匀的骰子,结果朝上的一面是6点,则从概率理论角度来讲,这一结果称为一个()。A:试验B:事件C:样本D:概率
独立投骰子两次,X,Y表示投出的点数,令A={X+y=10},B={X>Y},则P(A+B)=_______.
将一颗骰子抛掷1次,则得到的点数为偶数的概率为()
投掷两个均匀的骰子,已知点数之和是偶数,则点数之和为6的概率为()
设随机变量X,Y相互独立,且X~N(μ,σ2),Y在[a,b]区间上服从均匀分布,则D(X-2Y)=()。
抛掷一枚硬币,正面朝上还是反面朝上,这一现象符合正态分布。
将双曲线=a+b化直,需要作()变换。A、y′=B、x′=C、x′=axD、y′=by
设浮点数的格式为:阶码 5 位,尾数 6 位,均用补码表示,请计算 X+Y 和 X-Y。(阶码和尾数均用补码计算)。【**,★,包捷 4.8,编号 2.3】 X=-1.625,Y=5.25
假设随意地投掷一均匀骰子两次,则两次出现的点数之和为8的概率为()A、3/36B、4/36C、5/36D、2/36
掷一个骰子,任一面朝上这一事件的发生都是等概分布的,任一面朝上这一事件所获得的自信息量是()。A、1/6B、2/6C、-log2(1/6)D、-log2(2/6)
X,Y相互独立,且都服[0,1]上的均匀分布,则服从均匀分布的是().A、(X,Y)B、XYC、X+YD、X-Y
将一枚硬币重复掷n次,以X和Y分别表示正面向上和反面向上的次数,则X和Y的相关系数等于()。
设(X,Y)在由直线y=x,y=2-x,y=0所围的区域内服从均匀分布,则P{0.1
微分方程y″-6y′+9y=e3x(x+1)的特解形式应设为:()A、xe3x(ax+B.B、x2e3x(ax+B.C、C.e3x(ax+D、ae3xx3
单选题掷一个骰子,任一面朝上这一事件的发生都是等概分布的,任一面朝上这一事件所获得的自信息量是()。A1/6B2/6C-log2(1/6)D-log2(2/6)
问答题将一枚均匀骰子掷10次,X表示点数6出现的次数,用切比雪夫不等式可估计P{|X-E(X)|
单选题GDI环境中,窗口的坐标系是如何构成的()。A左上角为原点,x轴正方向为水平向右,y轴正方向为竖直朝上B中间为原点,x轴正方向为水平向右,y轴正方向为竖直朝上C左下角为原点,x轴正方向为水平向右,y轴正方向为竖直朝下D左上角为原点,x轴正方向为水平向右,y轴正方向为竖直向下
单选题将一枚硬币重复掷n次,以X和Y表示正面朝上和反面朝上的次数,则X、Y的相关系数等于( )。A1B-1C0D1/2
单选题微分方程y″-6y′+9y=e3x(x+1)的特解形式应设为:()Axe3x(ax+B.Bx2e3x(ax+B.CC.e3x(ax+Dae3xx3
单选题y=x+b中,为确保信息x的安全,b值应该()。A设为某一常数B设为零C设为变化值D设为x的倍数
问答题2.将一枚骰子连掷两次,以X表示两次所得的点数之和,以Y表示两次出现的最小点数,分别求X,Y的分布律.