设x1,x2,…,x9是从正态总体N(μ，0.62)中随机抽取的样本，样本均值为，μa是标准正态 分布的a分位数，则均值μ的0.90置信区间为（ ）。A. ±0.2u0.95 B.±0.2u0.90 C. ±0.6u0.90 D.±0.6u0.95
设x1,x2,…,x9是从正态总体N(μ，0.62)中随机抽取的样本，样本均值为
，μa是标准正态 分布的a分位数，则均值μ的0.90置信区间为（ ）。
A.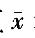
±0.2u0.95 B.
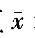±0.2u0.90 C. 
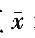±0.6u0.90 D.
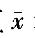±0.6u0.95
，μa是标准正态 分布的a分位数，则均值μ的0.90置信区间为（ ）。
A.
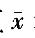±0.2u0.95 B.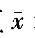±0.2u0.90 C. 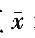±0.6u0.90 D.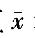±0.6u0.95参考解析
解析：当总体标准差σ已知时，利用正态分布可得μ的1-a置信区间为：
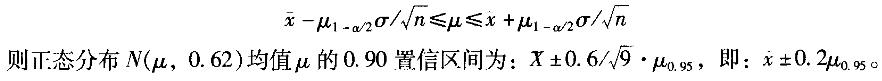
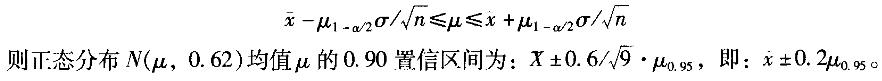
相关考题：
从任一非正态总体中随机抽取一个大样本观测“身高”变量,则以下正确的有() A.样本均值的抽样分布近似为F分布B.样本均值的抽样分布近似为卡方分布C.样本均值的抽样分布为严格的正态分布D.样本均值的抽样分布近似为正态分布E.样本数据有可能是正态分布
从一个正态总体中随机抽取一个容量为n的样本,其均值和标准差分别为50和8。当n=25时,构造总体均值μ的95%置信区间为()。 A、50±3.16B、50±4.97C、50±1.65D、50±1.96
对正态总体参数的估计描述正确的是（ ）。A.正态均值μ的无偏估计有两个，一个是样本均值的估计，另一个是样本中位数的估计，即B.对正态均值μ来说，样本均值总比样本中位数更有效，应舍去样本中位数C.在实际过程中，应优先选用样本均值去估计正态均值μ。但有时在现场，为了简便快捷，选用样本中位数去估计正态均值μ也是有的D.正态方差σ2的无偏估计常用的只有一个，就是样本方差S2E.正态方差σ2的无偏估计常用的只有一个，就是样本方差X2
已知总体分布为正态，方差未知。从这个总体中随机抽取样本容量为65的样本，样本平均数 为60，样本方差为100，那么总体均值 的99%的置信区间为A.[ 56.775 ,63.225]B.[53.550,66.450]C.[56.080,63.920]D.[57.550,62.450]
已知总体分布为正态，方差为100。从这个总体中随机抽取样本容量为16的样本，样本平均数为60，那么总体均值 的99%的置信区间为A.[50.10,69.90]B.[53.55,66.45]C.[56.08,63.92]D.[55.10,64.90]
已知正态总体标准差为10，样本量n=25，置信水平为95%，Z=1.96，样本均值=105.36。则以下正确的有（）A、样本均值的标准差为10B、样本均值的标准差为2C、样本均值的置信区间为（101.44，109.28）D、总体均值的置信区间为（101.44，109.28）
关于中心极限定理的描述正确的是：（）。A、对于n个相互独立同分布的随机变量共同服从正态分布，则样本均值又仍为正态分布B、正态样本均值服从分布N（μ，σ2/n）C、设X1，X2，„，Xn为n个相互独立共同分布随机变量，其共同分布不为正态分布或未知，但其均值和方差都存在，则在n相当大时，样本均值近似服从正态分布D、无论共同分布是什么，只要变量个数n相当大时，均值的分布总近似于正态分布
多选题已知正态总体标准差为10，样本量n=25，置信水平为95%，Z=1.96，样本均值=105.36。则以下正确的有（）A样本均值的标准差为10B样本均值的标准差为2C样本均值的置信区间为（101.44，109.28）D总体均值的置信区间为（101.44，109.28）