已知F=ABC+CD,下列使F=0的取值为( )。A. ABC=011 B.BC=11 C.CD=10 D. BCD=111
已知F=ABC+CD,下列使F=0的取值为( )。
A. ABC=011 B.BC=11 C.CD=10 D. BCD=111
A. ABC=011 B.BC=11 C.CD=10 D. BCD=111
参考解析
解析: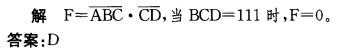
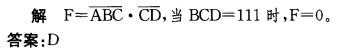
相关考题:
已知函数f(x)=㏑(x+2)-x2+bx+c, (1)若点P(-1,0)在f(x)的图象上,过点P的切线与直线y=-x+2平行,求f(x)的解析式;(2)若f(x)在区间[0,2]上单调递增,求b的取值范围。
已知二次函数f(x)的二次项系数为实数a,且其图像与直线2x+y=0交点横坐标为1和3. (1)若方程f(x)+6a=0有两个相等的实数根,求f(x)的解析式; (2)若f(x)的最大值为正数,求实数n的取值范围.
已知曲线,其中函数f(t)具有连续导数,且f(0)=0,f'(t)>0(0).若曲线L的切线与x轴的交点到切点的距离恒为1,求函数f(t)的表达式,并求以曲线L及x轴和y轴为边界的区域的面积.
已知函数 (1)求f(x)单调区间与值域; (2)设a≥1,函数g(x)=x3-3a2x-2a,x∈[0,1]。若对于任意x1∈[0,1],总存在x0∈[0,1]使g(x0)=f(x1)成立,求a的取值范围。
若已知力F对直角坐标系原点O的力矩矢的大小∣MO(F)∣,方向沿Oy向,则此力对此坐标系中各轴的矩为()。A、Mx(F)=0, My(F)=0,Mz(F)=0B、Mx(F)=0,M y(F)= ∣MO(F)∣,Mz(F) =∣MO (F)∣C、Mx(F)=0,My(F)= ∣MO(F)∣,MZ(F)=0D、Mx(F)=0,My(F)=0, Mz(F)= ∣MO(F)∣
已知f(t),为求f(t0-at),下列哪种运算顺序求得正确结果(式中t0、a都是正值,且a>1)? ()A、f(t)左移t0后反褶,在压缩a倍B、f(t)反褶左移t0后,在压缩a倍C、f(t)压缩a倍后反褶,在左移t0D、f(t)压缩a倍后反褶,在左移t0/a
单选题累积失效概率的取值范围为()。A0≥F≥1BF≥0C0≤F≤1DF≤100%