一绳缠绕在半径为r的鼓轮上,绳端系一重物M,重物M以速度v和加速度a向下运动(如图)。则绳上两点A、D和轮缘上两点B、C的加速度是( )。A、A、B两点的加速度相同,C、D两点的加速度相同B、A、B两点的加速度不相同,C、D两点的加速度不相同C、A、B两点的加速度相同,C、D两点的加速度不相同D、A、B两点的加速度不相同,C、D两点的加速度相同
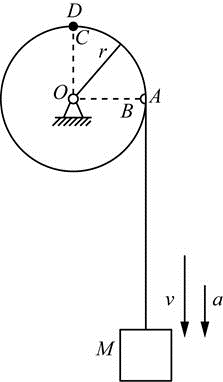
一绳缠绕在半径为r的鼓轮上,绳端系一重物M,重物M以速度v和加速度a向下运动(如图)。则绳上两点A、D和轮缘上两点B、C的加速度是( )。

A、A、B两点的加速度相同,C、D两点的加速度相同
B、A、B两点的加速度不相同,C、D两点的加速度不相同
C、A、B两点的加速度相同,C、D两点的加速度不相同
D、A、B两点的加速度不相同,C、D两点的加速度相同
B、A、B两点的加速度不相同,C、D两点的加速度不相同
C、A、B两点的加速度相同,C、D两点的加速度不相同
D、A、B两点的加速度不相同,C、D两点的加速度相同
参考解析
解析: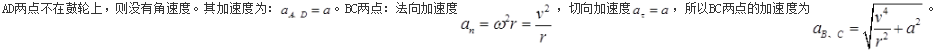
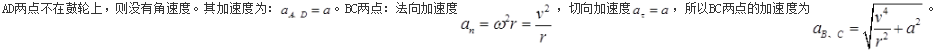
相关考题:
将绳绕在一个具有水平光滑轴的飞轮边缘上,如果在绳端挂一质量为m的重物时,飞轮的角加速度为α,如果以2mg的拉力代替重物拉绳时,飞轮的角加速度将[ ] A.小于αB. 大于α,小于2αC. 大于2αD. 等于2α
质量m1与半径r均相同的三个均质滑轮,在绳端作用有力或挂有重物,如图所示。已知均质滑轮的质量为m1=2kN·s^2/m,重物的质量分别为m2=2kN·s^2/m,m3=1kN·s^2/m,重力加速度按g=10m/s^2计算,则各轮转动的角加速度α间的关系是( )。 A. α1=α3>α2 B. α1<α2<α3 C. α1>α3>α2 D. α1≠α2=α3
图示两重物的质量均为m,分别系在两软绳上。此两绳又分别绕在半径各为r与2r,并固结在一起的两圆轮上。两圆轮构成的鼓轮的质量亦为m,对轴O的回转半径为ρ0外。两重物中一铅垂悬挂,一置于光滑平面上。当系统在左重物重力作用下运动时,鼓轮的角加速度α为:
两重物的质量均为m,分别系在两软绳上。此两绳又分别绕在半径各为r与2r并固结在一起的两轮上。两圆轮构成之鼓轮的质量亦为m,对轴O的回转半径为ρO。两重物中一铅垂悬挂,一置于光滑平面上。当系统在左重物重力作用下运动时,鼓轮的角加速度α为:
圆轮上绕一细绳,绳端悬挂物块。物块的速度v、加速度a。圆轮与绳的直线段相切之点为P,该点速度与加速度的大小分别为:A. vp = v,ap>a B. vp>v,apC. vp =v,app>v,ap>a
图示鼓轮半径r=3.65m,对转轴O的转动惯量JO= 0.92kg ? m2;绕在鼓轮上的绳端挂有质量m=30kg的物体A。不计系统质量与摩擦,欲使鼓轮以角加速度α=37.8rad/s2转动来提升重物,需对鼓轮作用的转矩M的大小是:A. 37.8N ? m B. 47N ? mC. 36.3N ? m D. 45.5N ? m
如图所示,墙上有两点M和N分别钉有两铁钉,M和N的连线与水平方向的夹角为45。,两者的高度差为l。一条不可伸长的轻质细绳一端同定于M点的铁钉上,另一端跨过N点的光滑铁钉悬挂一质量为m1的重物,在绳上距M点l/2的P点系上一质量为m2的重物.平衡后绳的MP段正好水平。则m1/m2为( )。 A.51/2B.5/21/2C.2D.21/2
将细绳绕在一个具有水平光滑轴的飞轮边缘上,现在在绳端挂一质量为m的重物,飞轮的角加速度为β,如果以拉力2mg代替重物拉绳时,飞轮的角加速度将()A、小于βB、大于β,小于2βC、大于2βD、等于2β
单选题图示鼓轮半径r=3.65m,对转轴O的转动惯量Jo=0.92kg·m 2;绕在鼓轮上的绳端挂有质量m=30kg的物体A。不计系统质量与摩擦,欲使鼓轮以角加速度α=37.8rad/s2转动来提升重物,需对鼓轮作用的转矩M的大小是:()A 37.8N.mB 47N.mC 36.3N.mD 45.5N.m