图示截面对z轴的惯性矩Iz为( )。
图示截面对z轴的惯性矩Iz为( )。

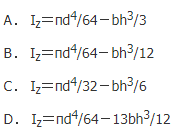

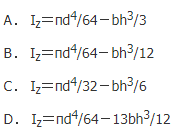
参考解析
解析:

相关考题:
已知平面图形的形心为C,面积为A,对Z轴的惯性矩为IZ,则图形对Z1轴的惯性矩为( )。A.IZ+B.2A.B.IZ+(A.+B.)2A.C.IZ+(A.2-B.2)A.D.IZ+(B.2-A.2)A.
图示a)、b)两截面,其惯性矩关系应为:A. (Iy)1>(Iy)2,(Iz)1 = (Iz)2B.(Iy)1=(Iy)2,(Iz)1>(Iz)2C. (Iy)1=(Iy)2,(Iz)1z)2D. (Iy)1y)2,(Iz)1 = (Iz)2
如图5-17所示,已知平面图形的形心为C,面积为A,对z轴的惯性矩为Iz,对图形z1轴的惯性矩有四种答案为( )。A. Iz + b2A B. Iz +(a + b)2 AC. Iz + (a2 -b2)A D. Iz+(b2 -a2)A
在平行移轴公式Iz1=Iz+a2A中,z轴和z1轴,z轴通过。()A、平行、中性轴B、平行、下边缘C、垂直、中性轴D、垂直、下边缘