图示四根细长(大柔度)压杆,弯曲刚度均为EI。其中具有最大临界荷载Fcr的压杆是( )。A.图(A)B.图(B)C.图(C)D.图(D)
图示四根细长(大柔度)压杆,弯曲刚度均为EI。其中具有最大临界荷载Fcr的压杆是( )。
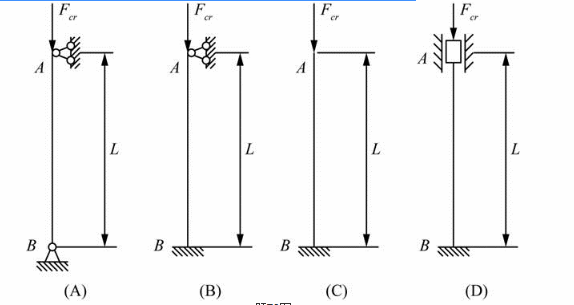

A.图(A)
B.图(B)
C.图(C)
D.图(D)
B.图(B)
C.图(C)
D.图(D)
参考解析
解析:方法一:根据欧拉公式,压杆的临界荷载Fcr=π2EI/(μl)2。式中,Fcr为临界载荷;E为压杆材料的弹性模量;I为截面的主惯性矩;l为压杆长度;μ为长度系数,与杆两端的约束条件有关。由题干可知,最大临界荷载Fcr只与长度系数μ有关,且成反比。A、B、C、D项的长度系数μ分别为1、0.7、2、0.5。因此,压杆的最大临界荷载Fcr由大到小为:图(D)>图(B)>图(A)>图(C)。
方法二:最大临界荷载与压杆长细比λ有关,当压杆几何尺寸相同时,长细比λ与压杆两端约束有关。图示中,图(A)有一个多余约束,图(B)有两个多余约束,图(C)没有多余约束,图(D)有三个多余约束。因此,杆件的稳定性:图(D)>图(B)>图(A)>图(C),即压杆的最大临界荷载Fcr由大到小为:图(D)>图(B)>图(A)>图(C)。
方法二:最大临界荷载与压杆长细比λ有关,当压杆几何尺寸相同时,长细比λ与压杆两端约束有关。图示中,图(A)有一个多余约束,图(B)有两个多余约束,图(C)没有多余约束,图(D)有三个多余约束。因此,杆件的稳定性:图(D)>图(B)>图(A)>图(C),即压杆的最大临界荷载Fcr由大到小为:图(D)>图(B)>图(A)>图(C)。
相关考题:
在材料相同的条件下,随着柔度的增大,()。 A.细长压杆的临界应力是减小的,中长压杆不是B.中长压杆的临界应力是减小的,细长压杆不是C.细长压杆和中长压杆的临界应力均是减小的D.细长压杆和中长压杆的临界应力均不是减小的
图示三根压杆均为细长(大柔度)压杆,且弯曲刚度均为EI。三根压杆的临界荷载Fcr的关系为:A. Fcra>Fcrb>FcrcB.Fcrb>Fcra>FcrcC. Fcrc>Fcra>FcrbD.Fcrb>Fcrc>Fcra
图示三根压杆均为细长(大柔度)压杆,且弯曲刚度均为EI。三根压杆的临界载荷Fcr的关系为( )。 A. Fcra>Fcrb>Fcrc B. Fcrb>Fcra>Fcrc C. Fcrc>Fcra>Fcrb D. Fcrb>Fcrc>Fcra
一端固定,一端自由的细长(大柔度)压杆,长为L [图5-71 (a)],当杆的长度减小一半时[图5-71 (b)],其临界载荷Fcr比原来增加( )。A. 4倍 B. 3倍 C. 2倍 D. 1倍
下列压杆的特性说法中错误的有()。A、临界力越小,压杆的稳定性越好,即越不容易失稳B、截面对其弯曲中性轴的惯性半径,是一个仅与横截面的形状和尺寸有关的几何量C、压杆的柔度λ综合反映了压杆的几何尺寸和杆端约束对压杆临界应力的影响D、压杆的柔度λ越大,则杆越细长,杆也就越容易发生失稳破坏
单选题压杆的柔度越大,压杆越(),临界应力越()。A细长,大B细长,小C粗短,大D粗短,小