图示截面,其轴惯性矩的关系为:
图示截面,其轴惯性矩的关系为:
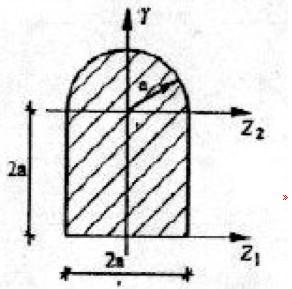



参考解析
解析:参照惯心矩的公式即可。
相关考题:
关于截面的几何性质,下列说法正确的是( )。A.图形对其对称轴的静矩为零,惯性矩不为零,惯性积为零B.图形对其对称轴的静矩不为零,惯性矩和惯性积均为零C.图形对其对称轴的静矩、惯性矩及惯性积均为零D.图形对其对称轴的静矩、惯性矩及惯性积均不为零
关梁的弯曲正应力,下列说法正确的是()。A、横截面上既有弯矩又有剪力的弯曲称为横力弯曲B、纯弯曲梁横截面上的正应力的大小与材料有关C、纯弯曲梁横截面某点的正应力与该横截面对中性轴的惯性矩成反比D、横力弯曲时,横截面将发生翘曲,使横截面为非平面E、纯弯曲梁横截面某点的正应力与该横截面对中性轴的惯性矩成正比
判断题截面图形对任一轴的惯性矩,都小于其对平行于该轴的形心轴的惯性矩。A对B错