图示机构中，曲柄OA＝r，以常角速度ω转动，则滑动机构BC的速度、加速度的表达式为（　　）。A．rωsinωt，rωcosωtB．rωcosωt，rω2sinωtC．rsinωt，rωcosωtD．rωsinωt，rω2cosωt

图示机构中，曲柄OA＝r，以常角速度ω转动，则滑动机构BC的速度、加速度的表达式为（　　）。

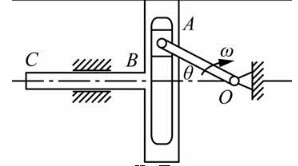
A．rωsinωt，rωcosωt
B．rωcosωt，rω2sinωt
C．rsinωt，rωcosωt
D．rωsinωt，rω2cosωt

参考解析

解析：由图可知滑动机构BC的速度、加速度与点A的水平分量相同。根据速度与角速度公式：vA＝rω，方向与曲柄OA垂直。由于曲柄OA以常角速度ω转动，因此角加速度为零，而切向加速度aA＝rω2，方向与曲柄OA垂直。因此，滑动机构BC的速度vBC＝vAsinθ＝rωsinωt，加速度aBC＝aAcosθ＝rω2cosωt。

相关考题：

杆OA绕固定轴O转动，长为l，某瞬时杆端A点的加速度a如题52图所示。则该瞬时OA的角速度及角加速度为（　　）。
查看答案
一平面机构曲柄长OA=r，以角速度ω0绕O轴逆时针向转动，在图示瞬时，摇杆O1N水平，连杆NK铅直。连杆上有一点D，其位置为DK=1/3NK，则此时D点的速度大小vD为：
查看答案
曲柄机构在其连杆AB的中点C与CD杆铰接，而CD杆又与DF杆铰接，DE杆可绕E点转动。曲柄OA以角速度ω= 8rad/s绕O点逆时针向转动。且OA = 25cm，DE=100cm。在图示瞬时，O、A、B三点共在一水平线上，B、E两点在同一铅直线上，∠CDE=90°，则此时DE杆角速度ωDE的大小和方向为：
查看答案
杆OA=l，绕固定轴O转动，某瞬时杆端A点的加速度a如图所示，则该瞬时杆OA的角速度及角加速度分别为：
查看答案
图示质量为m、长为l的杆OA以的角速度绕轴O转动，则其动量为：
查看答案
杆OA绕固定轴O转动，长为l。某瞬时杆端A点的加速度a如图所示，则该瞬时OA的角速度及角加速度为（　　）。
查看答案
图示四连杆机构OABO1中，OA=O1B=1/2AB=L，曲柄OA以角速度ω逆时针向转动。当φ=90%，而曲柄O1B重合于O1O的延长线上时，曲柄O1B上B点速度vB的大小和方向为：
查看答案
平面机构在图示位置时，AB杆水平，BC杆铅直，滑块A沿水平面滑动的速度vA≠0，加速度aA=0，则此时BC杆的角速度ωBC和角加速度αBC分别为：A.ωBC≠0,αBC≠0B. ωBC=0,αBC=0C. ωBC≠0,αBC=0D. ωBC=0,αBC≠0
查看答案
杆OA = l，绕固定轴O转动，某瞬时杆端A点的加速度a如图所示，则该瞬时杆OA的角速度及角加速度为：
查看答案
如图所示，曲柄OA长R，以匀角速度ω绕O轴转动，均质圆轮B在水平面上做纯滚动，其质量为m，半径为r。在图示瞬时，OA杆铅直。圆轮B对接触点C的动量矩为（　　）mRrω。A．0.5B．1.0C．1.5D．2.0
查看答案
杆OA绕固定轴0转动，长为l。某瞬时杆端A点的加速度a如图所示，则该瞬时OA 的角速度及角加速度为：
查看答案
曲柄OA在如图30-9所示瞬时以ω的角速度绕轴O转动，并带动直角曲杆O1BC在如图所示平面内运动。若取套筒A为动点，杆O1BC为动系，则牵连速度大小为（　　）。
查看答案
均质直角曲杆OAB的单位长度质量为ρ，OA=AB=2l，图示瞬时以角速度ω、角加速度α绕轴O转动，该瞬时此曲杆对O轴的动量矩的大小为：
查看答案
在图机构中，曲柄OA以匀角速度ω0转动，且OA=r，又AB=AC=r。当曲柄OA与连杆AB位于同一铅垂线上时，OA⊥0C，此时连杆AB的角速度为（　　）。
查看答案
四连杆机构如图所示，己知曲柄O1A长为r，且O1A＝O2B，O1O2＝AB＝2b，角速度为ω、角加速度为α，则M点的速度、切向和法向加速度的大小为（　　）。
查看答案
图示曲柄连杆机构中，OA=r，AB=2r，OA、AB及滑块B质量均为m，曲柄以ω的角速度绕O轴转动，则此时系统的动能为：
查看答案
如图4-71所示曲柄连杆机构中，OA=r，AB=2r，OA、 AB及滑块B质量均为m, 曲柄以ω的角速度绕O轴转动，则此时系统的动能为（ ）。
查看答案
图4-49所示机构中，曲柄OA以匀角速度绕O轴转动，滚轮B沿水平面作纯滚动，如图4-48所示。己知OA=l, AB=2l，滚轮半径为r。在图示位置时，OA铅直，滚轮B的角速度为（ ）。
查看答案
杆OA=l,绕固定轴O转动，某瞬时杆端A点的加速度a如图4-41所示，则该瞬时杆OA的角速度及角加速度为（ ）。
查看答案
刚体以角速度ω，角加速度ε绕定轴转动则在其转动半径为r处的线速度v=（），切线加速度at=（），法向加速度an=（）。
查看答案
填空题刚体以角速度ω，角加速度ε绕定轴转动则在其转动半径为r处的线速度v=（），切线加速度at=（），法向加速度an=（）。
查看答案
单选题平面机构在图示位置时，AB杆水平，BC杆铅直，滑块A沿水平面滑动的速度VA≠0，加速度aA=0，则此时BC杆的角速度wBC和角加速度αBC分别为：（）A wBC≠0，αBC≠0B wBC=0，αBC=0C wBC≠0，αBC=0D wBC=0，αBC≠0
查看答案
热门标签