如右图,正方形的迷你轨道边长为1米,1号电子机器人从点A以1米/秒的速度顺时针绕轨道移动,2号电子机器人从点A以3米/秒的速度逆时针绕轨道移动,则它们的第2017次相遇在:A.点AB.点CC.点BD.点D
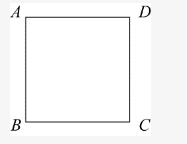
如右图,正方形的迷你轨道边长为1米,1号电子机器人从点A以1米/秒的速度顺时针绕轨道移动,2号电子机器人从点A以3米/秒的速度逆时针绕轨道移动,则它们的第2017次相遇在:

A.点A
B.点C
C.点B
D.点D
B.点C
C.点B
D.点D
参考解析
解析:第一步,本题考查行程问题,属于相遇追及类。
第二步,第1秒1号机器人顺时针走到点D,2号逆时针走到点D,故两个机器人每过1秒相遇一次,相遇点依次为D—C—B—A—D—C—B—A……每4次相遇为一个周期。
第三步,2017÷4=504…1,则第2017次相遇与第1次相遇地点是同一地点,即D点。
第二步,第1秒1号机器人顺时针走到点D,2号逆时针走到点D,故两个机器人每过1秒相遇一次,相遇点依次为D—C—B—A—D—C—B—A……每4次相遇为一个周期。
第三步,2017÷4=504…1,则第2017次相遇与第1次相遇地点是同一地点,即D点。
相关考题:
一列客车长250米,一列货车长350米,在平行的轨道上相向行驶,从两车头相遇到两车尾相离经过15秒,已知客车与货车的速度比是5∶3。问两车的速度相差多少?A.10米/秒B.15米/秒C.25米/秒D.30米/秒
如图5—17所示,在竖直平面内有一光滑的圆形轨道,轨道半径为尺,一个小球可在轨道内侧做圆周运动,且在通过圆周顶端的A点时不脱离轨道掉下来.(1)小球通过A点的最小速度V0为多大(2)在小球以速度V0通过A点的情况下,小球运动到B点时对轨道的压力F为多大
如图所示,在竖直平面内有一光滑的圆形轨道,轨道的半径为R,一小球可在轨道内侧做圆周运动,且在通过圆周顶端的A点时不脱离轨道掉下来。则:(1)小球通过A点的最小速度v0为多大?(2)在小球以速度v0通过A点的情况下,小球运动到B点时对轨道的压力F为多大?
一个山丘的形状如下图所示。甲乙两人同时从A点出发匀速前往B点,到达B点后立刻返回。甲上坡速度为3米/秒,下坡速度为5米/秒,乙上坡速度为2米/秒,下坡速度为3米/秒。问两人首次相遇时,距A点的路程为多少米?A.108B.138C.150D.162
如图,在△ABC中,AC=8,BC=6,∠ACB=90°,动点P以每秒一个单位的速度从点A出发,沿着边AC向点C移动,同时,动点Q以相同的速度从点B出发,沿着边BA向点A移动,设P,Q两点移动时间为t秒(0≤t≤8)。 (1)当t为何值时,△APQ的面积最大 最大值是多少 (2)以PC为直径的半圆交PQ于点D,是否存在t,使得PD=DQ 若存在,求出t的值,若不存在说明理由。
下图中ABCD为边长10米的正方形路线,E为AD中点,F为与B相距3米的BC上一点,从E点到F点有小路EGHF,小路的每一段都与AB垂直或平行,且GH相距2米。甲经EABF从E点匀速运动到F点用时9秒,则其以相同速度经EGHF从E点匀速运动到F点用时多少秒?A.12B.10C.9D.8
1675年,丹麦天文学家罗默在观测木星较大的卫星木卫1的食时,发现在地球远离木星时观测比在地球靠近木星时观测到的木卫1的食的时间要滞后大约1000秒左右,利用这个观测结果,我们可以推算出()。A、地球绕太阳的轨道运动速度B、木星绕地球的轨道运动速度C、木卫1绕木星的轨道运动速度D、光的速度
下列说法中正确的是哪一个()?A、原子轨道是电子运动的轨迹B、原子轨道是电子的空间运动状态,即波函数C、主量子数为3时,有3s、3p、3d三个轨道D、s轨道绕核旋转时,其轨道为一圆圈,而p电子的轨道为"8"字形
按玻尔的氢原子理论,电了在以质子为中心,半径为r的圆形轨道上运动,把这样一个原子放在均匀的外磁场中,使电子轨道平面与B垂直,在r不变的情况下,电子轨道运动角速度将()。A、增加B、减小C、不变D、改变方向
多选题关于地球在绕日公转的下列说法,正确的是()。A太阳中心位于地球轨道椭圆的一个焦点上,这一点也是其他行星轨道椭圆的焦点之一B公转是一种转动,即圆周运动C春分日,地球位于地球轨道椭圆的中距点D地球过近日点时,速度最快;而过远日点时,速度最慢,但面积速度不变
单选题A 不论在轨道1还是在轨道2运行,卫星在P点的速度都相同B 不论在轨道1还是在轨道2运行,卫星在P点的加速度都相同C 卫星在轨道1的任何位置都具有相同加速度D 卫星在轨道2的任何位置都具有相同动量
单选题地球绕日公转的过程中()A靠近A点时,角速度较快,线速度较慢B从A点到C点,太阳直射点在北半球并向北移动C地轴与公转轨道的夹角为23º26ˊD由于黄赤交角的存在,导致四季更替