如图,两个同心圆构成的圆环被均匀地分割成7份,连同中间的小圆共8个区域。若要给这8个区域着色,至少需要_______?种颜色,才能使相邻区域颜色不同。A.3B.4C.5D.6
如图,两个同心圆构成的圆环被均匀地分割成7份,连同中间的小圆共8个区域。若要给这8个区域着色,至少需要_______?种颜色,才能使相邻区域颜色不同。
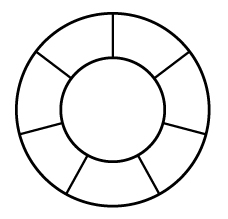

A.3
B.4
C.5
D.6
B.4
C.5
D.6
参考解析
解析:要求相邻区域颜色不同,优先涂相邻面最多的区域,即中间的圆。为了使得所用颜色最少,则其他7个区域涂色如下:
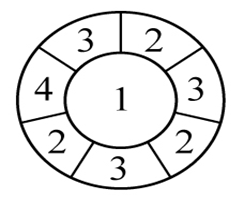
由上图可知,至少需要4种颜色。

由上图可知,至少需要4种颜色。
相关考题:
●试题五阅读下列程序说明和C代码,将应填入(n)处的字句写在答题纸的对应栏内。【程序5说明】著名的四色定理指出任何平面区域图均可用四种颜色着色,使相邻区域着不同的颜色。本程序对给定的区域图找出所有可能的不超过四种颜色的着色方案。程序中用1~4表示四种颜色。要着色的N个区域用0~N-1编号,区域相邻关系用adj[][]矩阵表示,矩阵的i行j列的元素为1,表示区域i与区域j相邻;矩阵的i行j列的元素为0,表示区域i与区域j不相邻。数组color[]用来存储着色结果,color[i]的值为区域i所着颜色。【程序5】#includestdio.h#define N 10void output(int color[])/*输出一种着色方案*/{int i;for(i=0;iN;i++)printf("%4d",color[i]);printf("\n");}int back(int*ip,int color[])/*回溯*/{int c=4;while(c==4){if(*ip=0)return 0;--(*ip);c= (1) ;color[*ip]=-1;}return c;}/*检查区域i,对c种颜色的可用性*/int color0k(int i,int c,int[][N],int color[]}{int j;for(j=0;ji;j++)if( (2) )return 0;return 1;}/*为区域i选一种可着的颜色*/int select(int i,int c,int adj[][N],int color[]){int k;for(k=c;k=4;k++)if(colorOK( (3) ))return k;return 0;}int coloring(int adj[][N])/*寻找各种着色方案*/{int color[N],i,c,cnt;for(i=0;iN;i++)color[i]=-1;i=c=0;cnt=0;while (1) {if((c= (4) )==0){c=back(i,color);if(c==0)return cnt;}else{ (5) ;i++;if(i==N){output(color);++cnt;c=back(i,color);}else c=0;}}}void main(){int adj[N][N]={{0,1,0,1,1,1,1,1,1,1},{1,0,1,1,0,1,1,1,1,0},{0,1,0,1,0,1,1,0,1,1},{1,1,1,0,1,1,0,0,1,1},{1,0,0,1,0,1,0,0,0,0},{1,1,1,1,1,0,1,0,0,1},{1,1,1,0,0,1,0,0,1,0},{1,1,0,0,0,0,0,0,1,1},{1,1,1,1,0,0,1,1,0,1},{1,0,1,1,0,1,0,1,1,0}};printf("共有%d组解.\n",coloring(adj));}
阅读下列程序说明和C代码,将应填入(n)处。【程序5说明】著名的四色定理指出任何平面区域图均可用四种颜色着色,使相邻区域着不同的颜色。本程序对给定的区域图找出所有可能的不超过四种颜色的着色方案。程序中用1~4表示四种颜色。要着色的N个区域用0~N-1编号,区域相邻关系用 adj[][]矩阵表示,矩阵的i行j列的元素为1,表示区域i与区域j相邻;矩阵的i行j列的元素为0,表示区域i与区域j不相邻。数组color[]用来存储着色结果,color[i]的值为区域i所着颜色。【程序5】include<stdio.h>define N 10void output(int color[])/*输出一种着色方案*/{ int i;for(i=0;i<N;i++)printf("%4d",color[i]);printf("\n");}int back (int * ip,int color[])/*回溯*/{ int c=4;while(c==4){if(*ip<=0)return 0;--(*ip);c=(1);color[*ip]=-1;}return c;}/*检查区域i,对c种颜色的可用性*/int colorOk(int i,int c,int [][N],int color[]}{ int j;for(j=0;j<i;j++)if((2))return 0;return 1;}/*为区域i选一种可着的颜色*/int select (int i,int c,int adj[][N],int color[]){ int k;for(k=c;k<=4;k++)if(colorOK((3)))return k;return 0;}int coloring(int adj[][N])/*寻找各种着色方案*/{ int color[N],i,c,cnt;for(i=0;i<N;i++)color[i] =-1;i=c=0;cnt=0;while(1){if((c=(4))==0){c=back(i,color);if(c==0)return cnt;}else{(5);i++;if(i==N){output(color);++cnt;c=back(i,color);}else c=0;}}}void main(){ int adj[N][N]={{0,1,0,1,1,1,1,1,1,1},{1,0,1,1,0,1,1,1,1,0},{0,1,0,1,0,1,1,0,1,1},{1,1,1,0,1,1,0,0,1,1},{1,0,0,1,0,1,0,0,0,0},{1,1,1,1,1,0,1,0,0,1},{1,1,1,0,0,1,0,0,1,0},{1,1,0,0,0,0,0,0,1,1},{1,1,1,1,0,0,1,1,0,1},{1,0,1,1,0,1,0,1,1,0}};printf("共有%d组解.\n",coloring(adj));}
请阅读以下技术说明和C代码,将程序段中(1)~(5)空缺处的语句填写完整。【说明】著名的四色定理指出任何平面区域图均可用4种颜色着色,使相邻区域着不同的颜色。以下C程序对给定的区域图找出所有可能的不超过4种颜色的着色方案。该程序中用1~4分别表示4种颜色。要着色的N个区域用0~-1编号,区域相邻关系用adj[][]矩阵表示,矩阵的i行j列的元素为1,表示区域i与区域了相邻;矩阵的i行j列的元素为0,表示区域i与区域j不相邻。数组color[]用来存储着色结果,color[i]的值为区域i,所着颜色。【C程序】include <stdio.h>define N 10void output(int color[]) { /*输出一种着色方案*/int i ;for ( i = 0 ; i < N ; i++ )printf( "%4d" , color[i] ) ;printf ("\n") ;}int back(int *ip ,int color[] ) { /*回溯*/intc = 4 ;while ( c == 4 ) {if ( *ip <= 0 )return 0 ;-- (*ip) ;c =(1);color[*ip] =-1 ;}return c ;}/*检查区域i,对c种颜色的可用性*/int colorOk(int i , intc , int [] [N] ,int color[ ] ) {int j ;for (j = 0 ; j < i ; j++ )if ( (2) )return 0 ;return 1 ;}/*为区域i选一种可着色的颜色*/int select (int i ,int c ,int adj [] [N] ,int color[ ] ){int k ;for(k = c ; k <= 4 ; k++ )if( colorOK( (3) ))return k ;return 0 ;}int coloring(int adj [] [N]) { /*寻找各种着色方案*/int color[N] , i , c , cnt ;for(i = 0 ; i < N ; i++)color[i] =-1 ;i = c = 0 ;cnt = 0 ;while(1) {if((c =(4) ) == 0 {c = back( i , color);if( c == 0 )return cnt;}else {(5);i++ ;if i == N) {output(color);++cnt ;c = back( i , color ) ;}else c = 0 ;}}}void main()(int adj[N] [N] ={ {0,1,0,1,1,1,1,1,1,1},{1,0,1,1,0,1,1,1,1,0},{0,1,0,1,0,1,1,0,1,1},{1,1,1,0,1,1,0,0,1,1},{1,0,0,1,0,1,0,0,0,0},{1,1,1,1,1,0,1,0,0,1},{1,1,1,0,0,1,0,0,1,0},{1,1,0,0,0,0,0,0,1,1},{1,1,1,1,0,0,1,1,0,1},{1,0,1,1,0,1,0,1,1,0},} ;printf("共有%d组解.\n",coloring(adj));}
阅读下列程序说明和C代码,将应填入(n)处的字句写在对应栏内。【程序说明】著名的四色定理指出任何平面区域图均可用4种颜色着色,使相邻区域着不同的颜色。本程序对给定的区域图找出所有可能的不超过4种颜色的着色方案。程序中用1~4表示4种颜色。要着色的N个区域用0~N-1编号,区域相邻关系用adj[][]矩阵表示,矩阵的i行j列的元素为1,表示区域i与区域j相邻:矩阵的i行j列的元素为0,表示区域i与区域j不相邻。数组color[]用来存储着色结果,color[i]的值为区域i所着颜色。【程序】include<stdio.h>define N 10void output(int color[])/*输出一种着色方案*/{int i;for(i=0; i<N; i++)printf("%4d", color[i]);pfintf("\n");}int back(int *ip,int color[])/*回溯*/{int c=4;while(c==4){if(*ip<=0)return 0;--(*ip);c= (1);color[*ip]=-1;}return c;}/*检查区域i,对c种颜色的可用性*/int colorOK(int i, int c, int adj[][N], int color[]){int j;for(j=0; j<i; j++)if((2))return 0;return 1;}/*为区域i选一种可着的颜色*/int select(int i,int c,int adj[][N], int color[])int k;for(k = c; k<=4; k++)if( (3) )return k;return 0;int coloring(int adj[][N])/*寻找各种着色方案*/{int color[N], i, c, cnt;for(i=0; i<N; i++)cotor[i]=-1;i=c=0;cnt=0;while(1){if((c=(4)==0){c=back(i, color);if(c==0)return cnt;}else{(5); i++;if(i==N){output(color);++cnt;c=back(i, color);}else c = 0;}}}void main(){int adj[N][N]={{0,1,0,1,1,1,1,1,1,1},{1,0,1,1,0,1,1,1,1,0},{0,1,0,1,0,1,1,0,1,1},{1,1,1,0,1,1,0,0,1,1},{1,0,0,1,0,1,0,0,0,0},{1,1,1,1,1,0,1,0,0,1},{1,1,1,0,0,1,0,0,1,0},{1,1,0,0,0,0,0,0,1,1},{1,1,1,1,0,0,1,1,0,1},{1,0,1,1,0,1,0,1,1,0}};printf("共有%d组解.\n",coloring(adj));}
阅读以下说明和C语言函数,将应填入(n)处的语句写在对应栏内。【说明】著名的四色定理指出任何平面区域均可以用4种颜色着色,使相邻区域着不同的颜色。本程序对给定的区域图找出所有可能的不超过4种颜色的着色方案。【函数】include <stdio.h>define N 10 /*要着色的N个区域*/void output(int color[]) /*输出一种着色方案 color[i]的值为区域i所着颜色*/{int i;for (i=0; i<N; i++)printf("%4d", color[i]);printf("\n");}int back(int *ip, int color[j] /*回溯*/int c=4;while (c==4){if (*ip<=0)return 0:--(*ip);c=(1);color[*ip]=-1;}return c;}/*检查区域i,考查c种颜色的可能性 */int colorOK(iht i, int c, int adj[][N], int color[]){int j;for(j=0; j<i; j++)if ((2))return 0;return 1;}/*为区域i选一种可着的颜色*/int select(int i, int c, int adj[][N], int color[])/*寻找各种着色方案 adj[i][j]=1表示区域i与区域j不相邻*/{int k;for (k=c; k<=4; k++) /*4种颜色*/if (colorOK((3)))return k;return 0;}int coloring(int adj[][N]){int color[N], i, c, cnt;for (i=0; i<N; i++) color[i]=-1:i=c=0; cnt=0;while (1)[if ((c=(4))==0){c=back(i, color);if (c==0)return cnt;}else{(5);i++;if(i==N){output(color);++cnt;c=back(i, color);}elsec=0;}}}void main(){int adj[N][N]={ {0, 1, 0, 1, 1, 1, 1, 1, 1, 1},{1, 0, 1, 1, 0, 1, 1, 1, 1, 0},{0, 1, 0, 1, 0, 1, 1, 0, 1, 1},{1, 1, 1, 0, 1, 1, 0, 0, 1, 1},{1, 0, 0, 1, 0, 1, 0, 0, 0, 0},{1, 1, 1, 1, 1, 0, 1, 0, 0, 1},{1, 1, 1, 0, 0, 1, 0, 0, 1, 0},{1, 1, 0, 0, 0, 0, 0, 0, 1, 1},
如图所示,圆被三条线段分成四个部分。现有红、橙、黄、绿四种涂料对这四个部分上色,假设每部分必须上色,且任意相邻的两个区域不能用同一种颜色,问共有几种不同的上色方法? A. 64种B. 72种C. 80种D.96种
某沿海城市管辖7个县,这7个县的位置如图。现用红、黑、绿、蓝、紫五种颜色给图染色,要求任意相邻的两个县染不同颜色。共有多少种不同的染色方法?()A. 2400 B. 4860 C. 1920 D. 5760
单选题对比度控制()。A允许选择指定区域改变其色值B允许选定一种颜色通道调整色值C允许选定多种颜色通道调整色值D允许同时调整高亮区域、中间影调和阴影部分